こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。
本稿では、具体的な静電場の現象例として、線電荷のつくる静電場をみていきます。
線電荷のつくる静電場
例2.1(線電荷のつくる静電場)
無限に長い直線上における線密度\(\lambda\)の電荷分布は、直線との距離\(r\)の位置に、直線と垂直方向(符号つきで)外向き、大きさ\(\frac{\lambda}{2\pi \epsilon_0 r}\)の静電場をつくる。
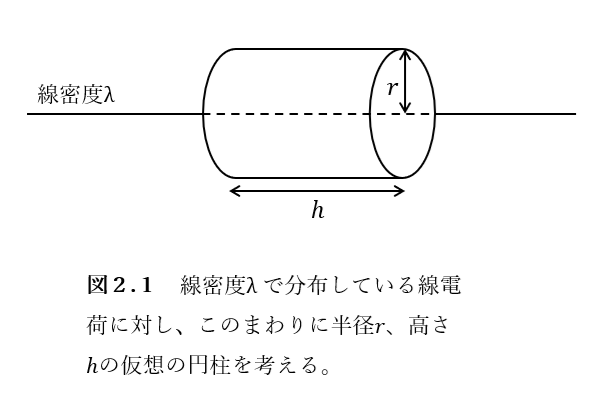
証明 空間の対称性より、電場のようすは直線との距離\(r\)にのみ依存し、直線と垂直方向(符号付きで)外向きになることが要請される。よって、直線を軸にした高さ\(h\)の図2.1のような仮想的な円柱に積分形のガウスの法則を適用すると、電場はこの側面のみをいたるところ垂直に貫くので、
$$
E(r)\cdot (2\pi rh)=\frac{\lambda h}{\epsilon_0}
$$より、整理すると題意が示される。□
別の証明 線は\(z\)軸方向に沿っていて、観測点は\(xy\)平面上の、線から距離\(r\)の点\(\boldsymbol{r}=(r,0,0)\)であるとする。微小線要素\(dz\)が観測点につくる微小電場は、クーロンの法則より、
$$
dE=\frac{1}{4\pi \epsilon_0}\frac{\lambda dz}{r^2+z^2}
$$とかけ、ここで対称性より\(z\)方向の成分は相殺されるので、微小電場の直線と垂直方向(符号付きで)外向きの成分のみ残すと、
$$
dE_r=\frac{1}{4\pi \epsilon_0}\frac{\lambda dz}{r^2+z^2}\frac{r}{\sqrt{r^2+z^2}}=\frac{\lambda r}{4\pi \epsilon_0}\frac{dz}{(r^2+z^2)^{3/2}}
$$観測点の全電場の半径成分は、線の全長にわたってこの式を積分したものであるので、
$$
E=\frac{\lambda r}{4\pi \epsilon_0} \displaystyle \int_{-\infty}^{\infty}\frac{dz}{(r^2+z^2)^{3/2}}=\frac{\lambda}{2\pi \epsilon_0 r}
$$として、示された。□
以上、線電荷のつくる静電場になります。


コメント