静電場(理論編1)

こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

本稿で出てくる物理量の定義
・電場\(\mathbf{E}\) ; 電荷\(q\)が電気的に力\(\mathbf{F}\)を受けるとき、\(\mathbf{E} = \frac{\mathbf{F}}{q}\)として与えられる、空間の各位置がもつ性質。
・電位\(\phi\) ; 単位電荷を、考えている位置から基準点まで運ぶとき、電気的になされる仕事。
・電束 ; 電荷からその電荷の量だけ出る仮想の線。
・電束密度\(\mathbf{D}\) ; 空間の各位置における電束の密度。
・磁場\(\mathbf{H}\) ; 磁極\(m\)が磁気的に力\(\mathbf{F}\)を受けるとき、\(\mathbf{H} = \frac{\mathbf{F}}{m}\)として与えられる、空間の各位置がもつ性質。
・磁束 ; 磁荷からその磁荷の量だけ出る仮想の線。
・磁束密度\(\mathbf{B}\) ; 空間の各位置における磁束の密度。
・電荷分布\(\rho\) ; その位置での電荷分布を示す。
・電流\(\mathbf{i}\) ; 正電荷の流れる方向を向き、単位時間あたりに通過する電荷量を大きさとするベクトル量。
・電流密度\(\mathbf{J}\) ; 正電荷の流れる方向を向き、単位面積あたりに流れる電流の量を大きさとするベクトル量。
本稿で述べていることはすべて分極の生じない自由空間中での記述であるとする←真空中と思ってよい。

この記事の目次
▶ 電磁気学概観
▶ 静電場
　・本稿の最終的な結論
　・①クーロンの法則
　・②ガウスの法則ー積分形と微分形
　・③渦なしの法則ー積分形と微分形
　・④電位
　・⑤ポアソンの方程式
▶ 総括

電磁気学概観
高校での電磁気学は、法則性の読めないたくさんの公式をこねくり回していました。しかし実は、電磁気学全体の現象は、分極の生じない自由空間において成立する以下の４式で理論的にすべて説明されうることがわかっています。これらは一般に、マクスウェル方程式とよばれています。

$$
\left\{
\begin{aligned}
&\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0} \\
&\nabla \cdot \mathbf{B} = 0 \\
&\nabla \times \mathbf{E} = – \frac{\partial \mathbf{B}}{\partial t} \\
&\nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}
\end{aligned}
\right.
$$

演算子などの説明は他の記事に回すことにして、本稿ではとくに空間に静電場のみ形成されているとき(つまり、静止した電荷分布が形成されているとき)について詳しく考えていこうと思っています。

静電場
先に述べた静止した電荷分布が形成されているという仮定は物理的には、磁場が存在せず電場の時間微分も０であることに等しいので、第２式と第４式は両辺０になり、残った第１式と第３式のみが意味を持ちます。

$$
\left\{
\begin{aligned}
&\nabla \cdot \mathbf{E} = \frac{\rho}{\epsilon_0} \\
&\nabla \times \mathbf{E} = \mathbf{0}
\end{aligned}
\right.
$$

静電場はこの２式のみで記述される、つまり、空間中の電荷分布を１つに定めると、この２式から空間中の静電場が１つに定まってしまうということなのです。
実際にはこの方程式を連立して解くことはせず、この２式と等価である以下の２式を使います。

$$
\left\{
\begin{aligned}
&- \nabla^2 {\phi} = \frac{\rho}{\epsilon_0} \\
&\mathbf{E} = – \nabla {\phi}
\end{aligned}
\right.
$$

この第１式は偏微分方程式であって、一般にポアソンの方程式とよばれています。空間中の電荷分布を１つに定めると、ポアソンの方程式の解\(\phi\)が一つに定まり、これの勾配の逆符号をとれば直ちに静電場\(\mathbf{E}\)が定まるといった感じですね。

、、、とここまで天下り式に書いてきましたが、マクスウェル方程式が成り立つ理由だったり、等価な式へと変形する行間がわからなければ納得ができません。そもそも電荷分布がわかればクーロンの法則から静電場がわかるじゃないかというもっともな指摘もあるでしょう。このあたりを今から本稿で見ていきます。とはいえ、議論がよくわからなくなったときは、最終的な結論は先に出しておくので時折思い出して整理してみてください。これを目指して議論をしていきます。

本稿の最終的な結論
分極の生じない自由空間において空間中の電荷分布がわかっているとき、以下を解いて求めた空間中の静電場と、クーロンの法則を用いて求めた空間中の静電場は等しい。
$$
\left\{
\begin{aligned}
&- \nabla^2 {\phi} = \frac{\rho}{\epsilon_0} \\
&\mathbf{E} = – \nabla {\phi}
\end{aligned}
\right.
$$

1 クーロンの法則
クーロンの法則と重ね合わせの原理は、いずれも実験則であって、認めるしかないですね(本稿の議論もここから始めます)。

クーロンの法則 ; 距離\(R\)離れた２つの点電荷\(q_1\),\(q_2\)の間にはたらく力\(\mathbf{f}\)は、大きさが
$$
f=\frac{|q_1q_2|}{4\pi\epsilon_0 R^2}
$$であって、お互いを結ぶ直線方向に、\(q_1\)と\(q_2\)が同符号なら引力、異符号なら斥力として現れる。

重ね合わせの原理 ; ３つの電荷\(q\),\(q_1\),\(q_2\)が存在するときに\(q\)のうける電気的な力は、\(q\),\(q_1\)のみが存在するとき\(q\)が\(q_1\)から受ける力と、\(q\),\(q_2\)のみが存在するとき\(q\)が\(q_2\)から受ける力のベクトル和である。

これら実験則と、電場の定義（電荷\(q\)が電気的に力\(\mathbf{F}\)を受けるとき、\(\mathbf{E} = \frac{\mathbf{F}}{q}\)として与えられる、空間の各位置がもつ性質）から、静電場について以下がいえます。

位置\(\mathbf{r_1}\),\(\mathbf{r_2}\),…,\(\mathbf{r_n}\)に、点電荷\(q_1\),\(q_2\),…,\(q_n\)が静止しているとき、位置\(\mathbf{r}\)における電場は
$$
\mathbf{E(\mathbf{r})}=\sum_{1\le i\le n} \frac{q_i}{4\pi\epsilon_0} \frac{\mathbf{r}-\mathbf{r_i}}{|\mathbf{r}-\mathbf{r_i}|^3}
$$

ここからさらにもう少し状況を発展させて、空間領域\(V’\)に電荷が連続的に分布していることを考えてみます。空間領域\(V’\)を微小体積\(\Delta V’\)に分割することを考え、またある位置\(\mathbf{r’}\)における電荷密度を\(\rho(\mathbf{r’})\)とすると、この状況は点電荷\(\rho(\mathbf{r’})\Delta V’\)の集まりとみなせますよね。つまり
$$
\mathbf{E(\mathbf{r})}\simeq\sum \frac{\rho(\mathbf{r’})\Delta V’}{4\pi\epsilon_0} \frac{\mathbf{r}-\mathbf{r’}}{|\mathbf{r}-\mathbf{r’}|^3}
$$が成り立つということです。等号は\(\Delta V’\rightarrow0\)のときに厳密に成立し、このとき右辺は空間領域\(V’\)における体積分になります←こういう議論は物理をしてるとよく出てきますね。

空間領域\(V’\)に電荷が連続的に分布しているとき、ある位置\(\mathbf{r’}\)における電荷密度を\(\rho(\mathbf{r’})\)とすると、位置\(\mathbf{r}\)における電場は
$$
\mathbf{E(\mathbf{r})}=\displaystyle \int_{V’} \frac{\rho(\mathbf{r’})dV’}{4\pi\epsilon_0} \frac{\mathbf{r}-\mathbf{r’}}{|\mathbf{r}-\mathbf{r’}|^3}
$$

ただしこれは理論上こうなるというだけで、実際に体積分を計算するのはあまりに式が煩雑すぎて難しいことが多いです。空間中の電荷分布がわかっているとき、もっと何か別の方法で静電場を調べる方法も探してみましょう←本稿の最終的な結論にたどり着くモチベーションですよ、、、

2 ガウスの法則
以下の法則を、(積分形の)ガウスの法則といいます。

任意の閉曲面\(S\)の内部に存在する電荷の合計を\(q\)とする。閉曲面上の各位置\(\mathbf{r}\)における電場を\(\mathbf{E(\mathbf{r})}\)、面に垂直で閉曲面を外向きに貫く大きさ１のベクトルを\(\mathbf{n(\mathbf{r})}\)とすると、
$$
\displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS = \frac{q}{\epsilon_0}
$$

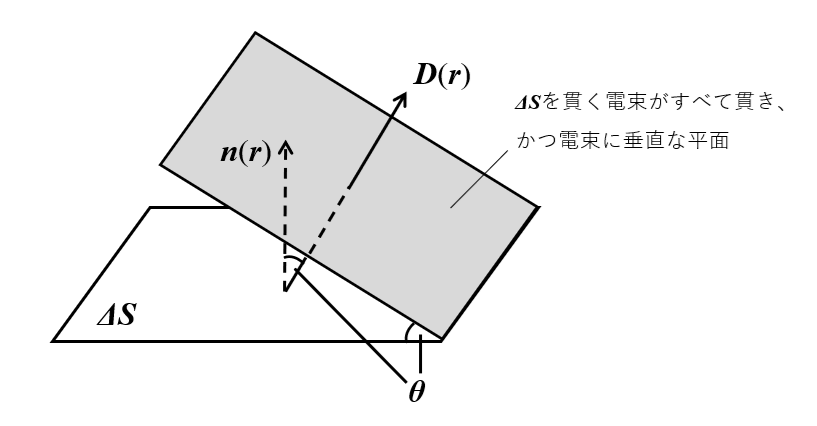
クーロンの法則からガウスの法則を示すことができる。
(i)空間中で閉曲面\(S\)内にただ１つ点電荷\(q\)が存在するとき、ガウスの法則が満たされることを示す。点電荷から等方的に\(q\)本の電束が飛び出ている(負電荷なら吸い込まれる)とすると、閉曲面を外向きに貫く電束の数\(N\)は明らかに\(q\)本である。一方で閉曲面上の微小面\(\Delta S\)を考えると、この微小面を外向きに貫く電束の数\(\Delta N\)の絶対値は、(電束密度の大きさ)×(\(\Delta S\)を貫く電束がすべて貫き、かつ電束に垂直な平面の面積)であるので←先の図を参照、
$$
|\Delta N| \simeq |\mathbf{D(\mathbf{r})}| \Delta S cos\theta
$$点電荷から距離\(r\)離れたところでの、電束密度の大きさは等方性より、\(\frac{q}{4\pi r^2}\)であって、クーロンの法則より、点電荷から距離\(r\)離れたところでの、電場の大きさは、\(\frac{q}{4\pi\epsilon_0 r^2}\)であるので、向きも考えると、
$$
\mathbf{D(\mathbf{r})}=\epsilon_0 \mathbf{E(\mathbf{r})}
$$したがって、面に垂直で閉曲面を外向きに貫く大きさ１のベクトルを\(\mathbf{n(\mathbf{r})}\)とすると、
$$
|\Delta N|\simeq \epsilon_0 |\mathbf{E(\mathbf{r})}| \Delta S cos\theta = \mathbf \epsilon_0 {E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} \Delta S
$$これを\(\Delta V’\rightarrow0\)として面積分すると、閉曲面を外向きに貫く電束の数になるので、
$$
N = \displaystyle \int_{S} dN = \epsilon_0 \displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS = q
$$として示された。

(ii)空間中で閉曲面\(S\)外にただ１つ点電荷\(q\)が存在するとき、ガウスの法則が満たされることを示す。点電荷から等方的に\(q\)本の電束が飛び出ている(負電荷なら吸い込まれる)とすると、閉曲面を内向きに貫いて閉曲面内に入ってくる電束はすべて、いずれ外へ貫いて出ていくので、閉曲面を外向きに貫く電束の数\(N\)は0本である。一方で、(i)と同様に閉曲面を外向きに貫く電束の数\(N\)は、
$$
N = \epsilon_0\displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS
$$とも表せるから、
$$
N = \epsilon_0\displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS = 0
$$として示された。

ここで任意の電荷分布は、微小空間に分けていくと点電荷の集まりとみなせることは、先に述べたとおりである。任意の電荷分布が、閉曲面\(S\)内の点電荷\(q_1\),\(q_2\),…\(q_i\),…と閉曲面\(S\)外の点電荷\(Q_1\),\(Q_2\),…\(Q_j\),…の集まりとみなせると考える。このとき、\(q_1\),\(q_2\),…\(q_i\),…がそれぞれ単独で作る電場を\(\mathbf{e}_1\),\(\mathbf{e}_2\),…\(\mathbf{e}_i\),…とし、\(Q_1\),\(Q_2\),…\(Q_j\)がそれぞれ単独で作る電場を\(\mathbf{E}_1\),\(\mathbf{E}_2\),…\(\mathbf{E}_j\),…としたとき、ある位置\(\mathbf{r}\)での電場は、
$$
\mathbf{E}(\mathbf{r}) = \sum_{i} \mathbf{e}_i(\mathbf{r}) + \sum_{j} \mathbf{E}_j(\mathbf{r})
$$と表せることに注意する。
閉曲面\(S\)に対して\(\epsilon_0\displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS\)の値を求めると、(i),(ii)より各\(i\),\(j\)に対して\(\epsilon_0\displaystyle \int_{S} \mathbf{e}_i(\mathbf{r}) \cdot \mathbf{n(\mathbf{r})} dS = q_i\),\(\epsilon_0\displaystyle \int_{S} \mathbf{E}_j(\mathbf{r}) \cdot \mathbf{n(\mathbf{r})} dS = 0\)であることから、
$$
\epsilon_0\displaystyle \int_{S} \mathbf{E}(\mathbf{r}) \cdot \mathbf{n}(\mathbf{r}) dS = \epsilon_0\displaystyle \int_{S} (\sum_{i} \mathbf{e}_i(\mathbf{r}) + \sum_{j} \mathbf{E}_j(\mathbf{r})) \cdot \mathbf{n}(\mathbf{r}) dS = \epsilon_0(\sum_{i} {\displaystyle \int_{S} \mathbf{e}_i(\mathbf{r}) \cdot \mathbf{n(\mathbf{r})} dS} + \sum_{j} {\displaystyle \int_{S} \mathbf{E}_j(\mathbf{r}) \cdot \mathbf{n(\mathbf{r})} dS}) = \sum_i q_i
$$これは任意の電荷分布に対してガウスの法則が成立することを言っているので、示された。

あとの稿で話しますが、対称性のある電荷分布であれば、(積分形の)ガウスの法則を用いて静電場を求めることもできます。ですが、対称性のないランダムな電荷配置であったりすると、それは厳しいでしょう。これを解決するのが、以下に紹介する、空間を微小部分に分割して微小体積に対してガウスの法則を適用することで記述された、(微分形の)ガウスの法則です。

空間の各位置の電荷分布\(\rho(\mathbf{r})\)に対して、
$$
\nabla \cdot \mathbf{E} = \frac{\rho(\mathbf{r})}{\epsilon_0}
$$

**ところで、電磁気学において電場や磁場という概念を導入するのはどうしてでしょうか。実はニュートン以後しばらくは、クーロン力は、電荷や電流から電荷や磁極に互いに接することなく及ぼされるとされていて、電場という概念は存在しませんでした(遠隔作用の立場)。一方で、一般の力学や私たちの自然な考え方では、力は直接触れている他のものからのみ及ぼされるという理解の方が納得しやすいでしょう。これを踏まえてファラデーやマクスウェルがとったのは、電荷や電流が空間の性質を変え、この空間が力を順に伝えていき、他の電荷や磁極はそれが直接触れる周囲の空間から力を及ぼされるという立場でした(近接作用の立場)。この空間の性質が「場」なのです。
そうすると、積分形のガウスの法則は電荷とそれからかなり空間を離れた先にある電場が関係づけられていて、近接作用の立場に徹したものではありません。そこで、微小体積に対して局所的にガウスの法則を適用しようという、微分形のガウスの法則を考えるモチベーションが生まれるのです。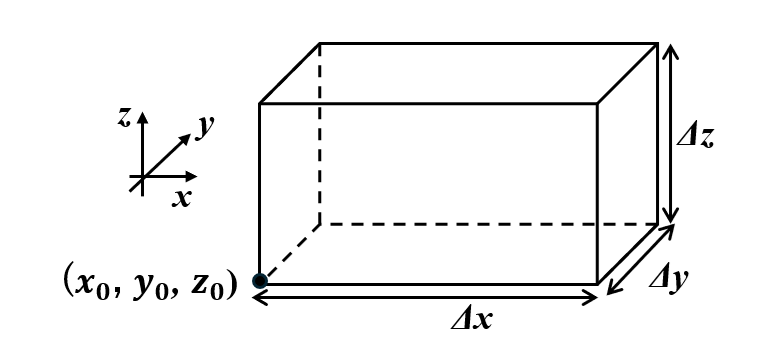

積分形のガウスの法則から微分形のガウスの法則を示すことができる。
微小体積として、各辺が\(\Delta x\),\(\Delta y\),\(\Delta z\)であるような図の直方体を考え、この閉じた面に対して、\(\displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS\)の値を求める。
\(x=x_0\)の面における\(\mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})}\)の面積分は、面に垂直な方向の電場成分が、電場のx成分の逆符号\(-E_x\)であることに注意すると、
$$
\displaystyle \int_{z_0}^{z_0+\Delta z} \int_{y_0}^{y_0+\Delta y} {-E_x(x_0,y,z)} dydz = \displaystyle \int_{0}^{\Delta z} \int_{0}^{\Delta y} -E_x(x_0,y_0+y’,z_0+z’) dy’dz’
$$ここで、各方向に偏微分可能な多変数関数\(f(x,y,z)\)について、\(\Delta x\),\(\Delta y\),\(\Delta z\)が微小ならば、一般に
$$
f(x+\Delta x,y+\Delta y,z\Delta z)\simeq f(x,y,z)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z
$$となるので、
$$
-E_x(x_0,y_0+y’,z_0+z’)\simeq -E_x(x_0,y_0,z_0)-\frac{\partial E_x}{\partial y}y’-\frac{\partial E_x}{\partial z}z’
$$であることをふまえると、\(x=x_0\)の面における\(\mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})}\)の面積分は、
$$
\displaystyle \int_{0}^{\Delta z} \int_{0}^{\Delta y} (-E_x(x_0,y_0,z_0)-\frac{\partial E_x}{\partial y}y’-\frac{\partial E_x}{\partial z}z’) dy’dz’
$$と近似される。同様に、\(x=x_0+\Delta x\)の面における\(\mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})}\)の面積分は、面に垂直な方向の電場成分が、電場のx成分\(E_x\)であることに注意すると、
$$
\displaystyle \int_{0}^{\Delta z} \int_{0}^{\Delta y} (E_x(x_0,y_0,z_0)+\frac{\partial E_x}{\partial x}\Delta x+\frac{\partial E_x}{\partial y}y’+\frac{\partial E_x}{\partial z}z’) dy’dz’
$$と近似される。
ゆえに、この２つの積分の和、つまり微小直方体に対する\(\displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS\)の値の、\(x\)軸に垂直な面からの寄与は、微小直方体の体積を\(\Delta V=\Delta x \Delta y \Delta z\)と表すと、
$$
\displaystyle \int_{0}^{\Delta z} \int_{0}^{\Delta y} \frac{\partial E_x}{\partial x}\Delta x dy’dz’ = \frac{\partial E_x}{\partial x} \Delta V
$$となる。同様にして、\(y\)軸や\(z\)軸に垂直な面からの寄与は、\(\frac{\partial E_y}{\partial y} \Delta V\) , \(\frac{\partial E_z}{\partial z} \Delta V\)となるので、等号は\(\Delta V’\rightarrow0\)のときに厳密に成立し、この微小直方体に対して、
$$
\displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS = (\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}) dV = \nabla \cdot \mathbf{E} dV
$$
積分形のガウスの法則より、この微小直方体の内部に存在する電荷の合計を\(q\)とするとき、閉曲面上の各位置\(\mathbf{r}\)における電場を\(\mathbf{E(\mathbf{r})}\)、面に垂直で閉曲面を外向きに貫く大きさ１のベクトルを\(\mathbf{n(\mathbf{r})}\)とすると、
$$
\displaystyle \int_{S} \mathbf{E(\mathbf{r})} \cdot \mathbf{n(\mathbf{r})} dS = \frac{q}{\epsilon_0}
$$が成り立つ。電荷の合計は微小直方体に対して、\(\rho(\mathbf{r}) dV\)と表せるので、以上を踏まえると、
$$
\nabla \cdot \mathbf{E} = \frac{\rho(\mathbf{r})}{\epsilon_0}
$$として示される。

3 渦なしの法則
続いて、空間に任意の電荷分布があるとき、適当に２点\(P\),\(Q\)を定めて、\(+1\)の点電荷を\(P\)から\(Q\)へ運ぶときの、電気的な力に釣り合わせる外力のする仕事を考えます。力学の時にやったように、重力や弾性力などは、始点と終点さえ定めればその間をどのような経路で運んだとしても釣り合わせる外力のする仕事は一定でしたよね(こういう力を保存力といいました)。一方、摩擦力などはこういう性質をもたず、仕事が経路に依存する力でした(こういう力を非保存力といいました)。クーロン力は実は保存力で、始点と終点さえ定めればその間をどのような経路で運んだとしても釣り合わせる外力のする仕事は一定な力です。これを示します。

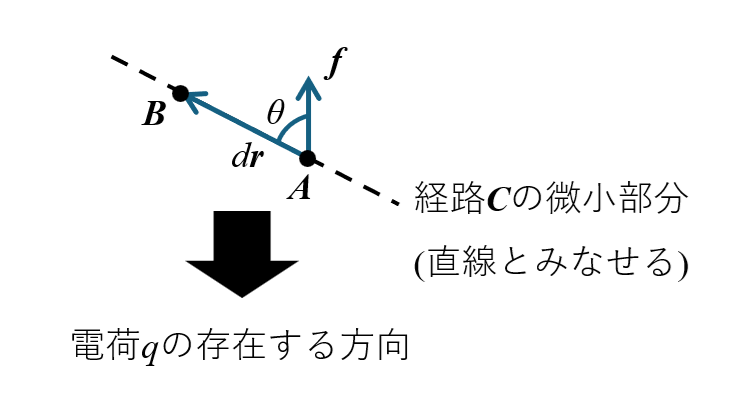
まず、空間中でただ１つ点電荷\(q\)が存在するときのクーロン力が保存力であることを示す。上の図において、点\(A\)、点\(B\)をそれぞれ点電荷\(q\)から、\(s\)、\(s+ds\)離れた点とする。このとき、経路\(C\)の微小区間、点\(A\)から点\(B\)上で電荷\(+Q\)を動かすときの仕事\(dw\)は、
$$
dw=\mathbf{f}(s) \cdot d\mathbf{r}=f(s)drcos\theta=f(s)ds
$$これは、点電荷から\(s\)離れた点から\(s+ds\)離れた点へ、直線的に遠ざけるときの仕事と等しい。これが任意の経路\(C\)上の各微小区間で成立することから、繰り返し用いると、点電荷から\(R\)離れた始点から、点電荷から\(R’\)離れた終点へ任意の経路で電荷\(+Q\)を動かしたときの仕事は、点電荷から\(R\)離れた点から、点電荷から\(R’\)離れた点へ、直線的に近づけるあるいは遠ざけるときの仕事に等しい。すなわち、仕事の値は、始点と終点の点電荷からの距離のみに依存するとして示された。

ここで任意の電荷分布は、微小空間に分けていくと点電荷の集まりとみなせることは、先に述べたとおりである。任意の電荷分布は点電荷\(q_1\),\(q_2\),…\(q_i\),…の集まりとし、\(q_1\),\(q_2\),…\(q_i\),…がそれぞれ単独で作る電場を\(\mathbf{e}_1\),\(\mathbf{e}_2\),…\(\mathbf{e}_i\),…とすると、始点\(X\)から終点\(Y\)まで任意の２経路\(C\),\(C’\)で電荷\(+Q\)を動かしたときの仕事は、
$$
-\displaystyle \int_{C} Q\mathbf{E}(\mathbf{r}) \cdot d\mathbf{r} = -\displaystyle \int_{C} Q (\sum_i\mathbf{e}_i(\mathbf{r})) \cdot d\mathbf{r} = -\sum_i \displaystyle \int_{C} Q\mathbf{e}_i(\mathbf{r}) \cdot d\mathbf{r} = -\sum_i \displaystyle \int_{C’} Q\mathbf{e}_i(\mathbf{r}) \cdot d\mathbf{r} = -\displaystyle \int_{C’} Q (\sum_i\mathbf{e}_i(\mathbf{r})) \cdot d\mathbf{r} = -\displaystyle \int_{C’} Q\mathbf{E}(\mathbf{r}) \cdot d\mathbf{r}
$$より等しいとして、クーロン力は保存力であることも示された。

クーロン力は保存力であることから、とくに始点と終点が等しいとき、つまり動かさないもしくは閉じた曲線を整数回回る経路で仕事は、つねに０であるといえます。これは電場の周回積分として、次のように表せます←とくに単位電荷を動かすことを考えます。

任意の静電場\(\mathbf{E(\mathbf{r})}\)について、以下が成立する。
$$
\oint_C \mathbf{E(\mathbf{r})} \cdot d\mathbf{r}=0
$$

これは、(積分形の)渦なしの法則ともよばれます。ガウスの法則のときと同じように、近接作用の立場に徹すると、微小体積に対して局所的に適用した渦なしの法則が有用であろうと予想できるでしょう。以下紹介するのが、(微分形の)渦なしの法則と呼ばれるものです。

任意の静電場\(\mathbf{E(\mathbf{r})}\)について、以下が成立する。
$$
\nabla \times \mathbf{E} = \mathbf{0}
$$

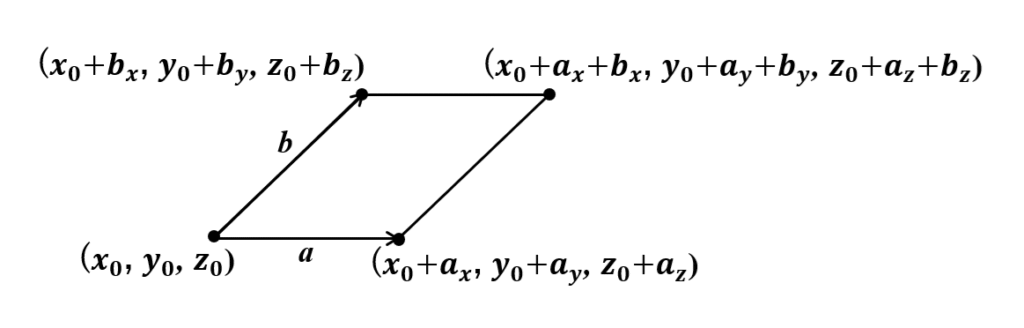
積分形のガウスの法則から微分形のガウスの法則を示すことができる。
微小経路として、各辺が\(a\),\(b\)であるような図の長方形を考え(ただし\(a\),\(b\)は微小)、この閉じた経路に対して、\(\oint_C \mathbf{E(\mathbf{r})} \cdot d\mathbf{r}\)の値を求める。なお、\(\mathbf{a}\),\(\mathbf{b}\)方向の単位ベクトルを、それぞれ\(\mathbf{e}_a\),\(\mathbf{e}_b\)としておく。(\(x_0\),\(y_0\),\(z_0\))から(\(x_0+a_x\),\(y_0+a_y\),\(z_0+a_z\))へ２点を結ぶ辺\(C\)に沿った電場の線積分は、
$$
\displaystyle \int_{C} \mathbf{E(\mathbf{r})} \cdot d\mathbf{r} = \displaystyle \int_{0}^{a} \mathbf{E}(x_0+te_{ax},y_0+te_{ay},z_0+te_{az}) \cdot \mathbf{e}_a dt = \displaystyle \int_{0}^{a} (\mathbf{E} \cdot \mathbf{e}_a)(x_0+te_{ax},y_0+te_{ay},z_0+te_{az}) dt
$$ここで、各方向に偏微分可能な多変数関数\(f(x,y,z)\)について、\(\Delta x\),\(\Delta y\),\(\Delta z\)が微小ならば、一般に
$$
f(x+\Delta x,y+\Delta y,z\Delta z)\simeq f(x,y,z)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z
$$となるので、
$$
(\mathbf{E} \cdot \mathbf{e}_a)(x_0+te_{ax},y_0+te_{ay},z_0+te_{az}) \simeq (\mathbf{E} \cdot \mathbf{e}_a)(x_0,y_0,z_0)+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_x}{\partial x}te_{ax}+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_y}{\partial y}te_{ay}+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_z}{\partial z}te_{az}
$$であることをふまえると、(\(x_0\),\(y_0\),\(z_0\))と(\(x_0+a_x\),\(y_0+a_y\),\(z_0+a_z\))の２点を結ぶ辺\(C\)に沿った電場の線積分は、
$$
\displaystyle \int_{0}^{a} [(\mathbf{E} \cdot \mathbf{e}_a)(x_0,y_0,z_0)+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_x}{\partial x}te_{ax}+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_y}{\partial y}te_{ay}+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_z}{\partial z}te_{az}]dt
$$と近似される。同様に、(\(x_0+a_x+b_x\),\(y_0+a_y+b_y\),\(z_0+a_z+b_z\))から(\(x_0+b_x\),\(y_0+b_y\),\(z_0+b_z\))へ２点を結ぶ辺\(C’\)に沿った電場の線積分は、
$$
-\displaystyle \int_{0}^{a} [(\mathbf{E} \cdot \mathbf{e}_a)(x_0,y_0,z_0)+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_x}{\partial x}(te_{ax}+b e_{bx})+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_y}{\partial y}(te_{ay}+b e_{by})+\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_z}{\partial z}(te_{az}+b e_{bz})]dt
$$と近似される。
ゆえに、この２つの和、つまり微小長方形に対する\(\oint_C \mathbf{E(\mathbf{r})} \cdot d\mathbf{r}\)の値の、\(\mathbf{a}\)に平行な辺からの寄与は、微小長方形の面積を\(\Delta S=ab\)と表すと、
$$
-\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_x}{\partial x}e_{bx} \Delta S -\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_y}{\partial y}e_{by} \Delta S -\frac{\partial (\mathbf{E} \cdot \mathbf{e}_a)_z}{\partial z}e_{bz} \Delta S = -\mathbf{e}_b \cdot \nabla (\mathbf{E} \cdot \mathbf{e}_a) \Delta S
$$となる。同様にして、\(\mathbf{b}\)に平行な辺からの寄与は、\(\mathbf{e}_a \cdot \nabla (\mathbf{E} \cdot \mathbf{e}_b) \Delta S\)となるので、等号は\(\Delta S\rightarrow0\)のときに厳密に成立し、この微小経路に対して長方形の大きさ１の法線ベクトルの一つを\(\mathbf{n}\)とすると、
$$
\oint_C \mathbf{E(\mathbf{r})} \cdot d\mathbf{r} = -\mathbf{e}_b \cdot \nabla (\mathbf{E} \cdot \mathbf{e}_a) dS + \mathbf{e}_a \cdot \nabla (\mathbf{E} \cdot \mathbf{e}_b) dS = (\nabla \times \mathbf{E}) \cdot \mathbf{n} dS
$$(最後の等号は計算を大幅に省略)となる。積分形の渦なしの法則より、
$$
\oint_C \mathbf{E(\mathbf{r})} \cdot d\mathbf{r}=0
$$が成り立つので、以上を踏まえると、
$$
(\nabla \times \mathbf{E}) \cdot \mathbf{n} dS = 0
$$ある経路における電場の回転を表すベクトル\(\nabla \times \mathbf{E}\)が、つねに\(\mathbf{n}\)と垂直、つまりつねに経路を含む平面内にあることは物理的に適当でないので、この式は
$$
(\nabla \times \mathbf{E}) = \mathbf{0}
$$と等価であるとして示される。

4 電位
静止した電荷分布が形成されているとき、始点と終点を定めると、それを結ぶ任意の経路で単位電荷を動かすときの、電気的な力に釣り合わせる外力の仕事が一意に定まるのは、先に述べたとおりです。このとき、始点として基準点\(\mathbf{r_0}\)を一つ決めると、始点から各位置\(\mathbf{r}\)へ任意の経路で単位電荷を動かすときの、電気的な力に釣り合わせる外力の仕事は、位置\(\mathbf{r}\)のみに依存して決まるといえますね。だから、この仕事の値を、\(\mathbf{r_0}\)を基準とした位置\(\mathbf{r}\)の電位\(\phi(\mathbf{r})\)と定義できるのです。電位について、以下が成り立ちます。

$$
\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})
$$

定義に従ってこれを示す。
位置(\(x\),\(y\),\(z\))から位置(\(x+\Delta x\),\(y\),\(z\))へ、単位電荷を動かすときの、電気的な力に釣り合わせる外力の仕事\(\Delta W\)は、\(\Delta x\)が微小であるとき、
$$
\Delta W \simeq -\mathbf{E}(x,y,z) \cdot \Delta x \mathbf{e}_x = – E_x(x,y,z) \Delta x
$$電位の定義より、位置(\(x\),\(y\),\(z\))から位置(\(x+\Delta x\),\(y\),\(z\))へ、単位電荷を動かすときの、電気的な力に釣り合わせる外力の仕事\(\Delta W\)は、位置(\(x\),\(y\),\(z\))を基準とした位置(\(x+\Delta x\),\(y\),\(z\))の電位\(\phi(x+\Delta x,y,z)-\phi(x,y,z)\)に等しいので、これより、
$$
E_x \simeq -\frac{\phi(x+\Delta x,y,z)-\phi(x,y,z)}{\Delta x}
$$等号は\(\Delta x \rightarrow 0\)のときに成立し、
$$
E_x = -\frac{\partial \phi}{\partial x}
$$\(y\)方向や\(z\)方向にも同様に、\(E_y = -\frac{\partial \phi}{\partial y}\)、\(E_z = -\frac{\partial \phi}{\partial z}\)が成立するので、
$$
\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})
$$として示される。

5 ポアソンの方程式
ここで、微分形のガウスの法則に対し、\(\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})\)を代入してみましょう。
$$
-\nabla \cdot \nabla \phi(\mathbf{r}) = -\nabla^2 \phi(\mathbf{r}) = \frac{\rho(\mathbf{r})}{\epsilon_0}
$$となりますよね。これこそ本稿のはじめの方に紹介したポアソンの方程式なのですが、電荷分布\(\rho(\mathbf{r})\)と定数分のずれ(積分定数)を決定する境界条件(無限遠や考えている境界における物理的に意味のある要請、くわしくは別稿で扱います)を与えたとき、解が一意に定まることが知られています。

ポアソンの方程式の解が、電荷分布\(\rho(\mathbf{r})\)と境界条件を与えたとき、一意に定まることを示す。
(i)電荷のないところでは、電位\(\phi(\mathbf{r})\)は極大や極小をとりえないことをいう。電荷のない位置\(\mathbf{r}\)で極値をとると仮定すると、２次微係数は０にはならないので、
$$
-\nabla^2 \phi(\mathbf{r}) \ne 0
$$これは位置\(\mathbf{r}\)に電荷がないため、\(\rho(\mathbf{r})=0\)より、
$$
-\nabla^2 \phi(\mathbf{r}) = 0
$$であることに矛盾する。よって仮定は誤りで、電荷のないところでは、電位\(\phi(\mathbf{r})\)は極大や極小をとりえないとして示される。

(ii)ある領域内に電荷がなく、またその領域の境界で電位\(\phi(\mathbf{r})\)が一定値\(\phi_0\)をとるとき、その領域全体で電位\(\phi(\mathbf{r})=\phi_0\)であることを示す。その領域中で電位\(\phi(\mathbf{r})=\phi_0\)でない位置\(\mathbf{r}\)があると仮定すると、領域内のどこかで電位\(\phi(\mathbf{r})\)が最大あるいは最小をとるが、これは(i)に矛盾する。よって仮定は誤りで、ある領域内に電荷がなく、またその領域の境界で電位\(\phi(\mathbf{r})\)が一定値\(\phi_0\)をとるとき、その領域全体で電位\(\phi(\mathbf{r})=\phi_0\)であるとして示される。

ここである電荷分布\(\rho(\mathbf{r})\)と境界条件に対して、\(\phi_1(\mathbf{r})\),\(\phi_2(\mathbf{r})\)がいずれもポアソンの方程式を満たすとする。このとき、
$$
-\nabla^2 \phi_1(\mathbf{r}) = \frac{\rho(\mathbf{r})}{\epsilon_0} , -\nabla^2 \phi_2(\mathbf{r}) = \frac{\rho(\mathbf{r})}{\epsilon_0}
$$であり、同じ境界条件を満たすことから、領域内のすべての位置で
$$
-\nabla^2 [\phi_1(\mathbf{r})-\phi_2(\mathbf{r})] = 0
$$かつ、境界で\(\phi_1(\mathbf{r})-\phi_2(\mathbf{r})=0\)を満たす。ゆえに、\(\phi_1(\mathbf{r})-\phi_2(\mathbf{r})\)は、領域内に電荷のないときのポアソンの方程式の１つの解である。(ii)より、ある領域内に電荷がなく、またその領域の境界で電位\(\phi(\mathbf{r})\)が一定値0をとるとき、その領域全体で電位0であるため、領域内のすべての位置で
$$
\phi_1(\mathbf{r})-\phi_2(\mathbf{r})=0
$$すなわち、ポアソンの方程式の解が、電荷分布\(\rho(\mathbf{r})\)と境界条件を与えたとき、一意に定まることが示された。

空間的な静電場のようす\(\mathbf{E}(\mathbf{r})\)は解\(\phi(\mathbf{r})\)の勾配の逆符号をとれば直ちに定まるので、結局以下の２式が空間中の電荷分布と境界条件を１つ与えたとき、空間中の静電場を１つに定めるのです。
$$
\left\{
\begin{aligned}
&- \nabla^2 {\phi} = \frac{\rho}{\epsilon_0} \\
&\mathbf{E} = – \nabla {\phi}
\end{aligned}
\right.
$$議論の過程をたどると、この２つの式は、クーロンの法則から導かれていますので、ここで出た解はクーロンの法則に矛盾しないものになります。よって、ポアソンの方程式と\(\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})\)から導かれる静電場\(\mathbf{E(\mathbf{r})}\)は、クーロンの法則から導かれるものと等しいという本稿の最終的な結論にたどり着くのです。

ところで、渦なしの法則と、\(\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})\)の関係はどうなっているのでしょうか。実は、\(\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})\)の式は渦なしの法則を含んでいます。以下に示します。

\(\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})\)が渦なしの法則を含むことを示す。電場の回転\(\nabla \times \mathbf{E}\)に、\(\mathbf{E} = – \nabla \phi\)を代入して計算すると、
$$
\nabla \times \mathbf{E}=-\nabla \times (\nabla \phi)
$$
この\(x\)成分は
$$
[-\nabla \times (\nabla \phi)]_x = -\frac{\partial}{\partial y}\frac{\partial \phi}{\partial z}+\frac{\partial}{\partial z}\frac{\partial \phi}{\partial y}
$$実用上一般に、多変数関数の偏微分の順序交換をしても、結果は等しくなるので、
$$
\frac{\partial}{\partial y}\frac{\partial \phi}{\partial z}=\frac{\partial}{\partial z}\frac{\partial \phi}{\partial y}
$$であることをふまえると、
$$
[-\nabla \times (\nabla \phi)]_x = 0
$$同様に、\(y\),\(z\)成分も０であるので、\(\nabla \times \mathbf{E}=0\)というのが自動的に出てくる。ゆえに、\(\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})\)が渦なしの法則を含むことが示された。

ポアソンの方程式と\(\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})\)の２式から、ガウスの法則と渦なしの法則の２式を導くことができ、逆もまた然りです。このため、ポアソンの方程式と\(\mathbf{E(\mathbf{r})} = – \nabla \phi(\mathbf{r})\)の２式と、ガウスの法則と渦なしの法則の２式は等価です。ゆえに理論上は、ガウスの法則と渦なしの法則の２式も、空間中の電荷分布を１つ与えたとき空間中の静電場を１つに定めることができます←この２式を一般に静電場の基本法則と呼んだりします。

総括
以上の一連の議論から、はじめの方に書いた本稿の最終的な結論が正しいことが示されました。一般には、点電荷の分布や対称性のある電荷分布を考えているときはクーロンの法則や(積分形の)ガウスの法則を、体積のある連続的な電荷の分布を考えているときはポアソンの方程式を使って静電場を求めることが多いなと思ってます(とくに現実には連続的な電荷の分布を考えることが多いので、ポアソンの方程式がはるかに扱いやすかったり)。とにかく、この結論を覚えておきましょう。

本稿の最終的な結論
分極の生じない自由空間において空間中の電荷分布がわかっているとき、
$$
\left\{
\begin{aligned}
&- \nabla^2 {\phi}(\mathbf{r}) = \frac{\rho(\mathbf{r})}{\epsilon_0} \\
&\mathbf{E}(\mathbf{r}) = – \nabla {\phi(\mathbf{r})}
\end{aligned}
\right.
$$を解いて求めた空間中の静電場と、クーロンの法則を用いて求めた空間中の静電場
$$
\mathbf{E(\mathbf{r})}=\displaystyle \int_{V’} \frac{\rho(\mathbf{r’})dV’}{4\pi\epsilon} \frac{\mathbf{r}-\mathbf{r’}}{|\mathbf{r}-\mathbf{r’}|^3}
$$は等しくなる。

次稿では、分極の生じない自由空間中ではないときについて考えます。ポアソンの方程式などを応用して、実際の電場を求める記事もいつか作ります。それではまたいつか。
↓↓↓しっかりと電磁気学を勉強したい初修の方は、紙の参考書を持っておくのもいいですよ！

電磁気学　1 電場と磁場 （物理入門コース） [ 長岡 洋介 ] 価格：2,640円（税込、送料無料) (2025/10/2時点) 楽天で購入

電磁気学　2 変動する電磁場 （物理入門コース） [ 長岡 洋介 ] 価格：1,980円（税込、送料無料) (2025/10/2時点) 楽天で購入