ビオサバールの法則を仮定したときの磁場におけるガウスの法則の証明

クーロンの法則と重ね合わせの原理より、任意の位置\(\mathbf{r}\)における静電場\(\boldsymbol{E}(\boldsymbol{r})\)は、以下のように書ける。
$$
\boldsymbol{E}(\boldsymbol{r})=\frac{q}{4\pi \epsilon_0}\frac{\boldsymbol{r}-\frac{\boldsymbol{d}}{2}}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}+\frac{-q}{4\pi \epsilon_0}\frac{\boldsymbol{r}+\frac{\boldsymbol{d}}{2}}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|^3} = \boldsymbol{r} \left\{ \frac{q}{4\pi \epsilon_0}\left( \frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}-\frac{1}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|^3}\right) \right\} – \frac{\boldsymbol{d}}{2} \left\{ \frac{q}{4\pi \epsilon_0} \left( \frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}+\frac{1}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|^3} \right) \right\}
$$\(\frac{d}{r}\ll 1\)であることから、微小項の２次以上を切り捨て、さらに１次の項までテイラー展開すると、それぞれ以下のように近似される。
$$
\frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}= \left\{ \left(\boldsymbol{r}-\frac{\boldsymbol{d}}{2}\right) \cdot \left(\boldsymbol{r}-\frac{\boldsymbol{d}}{2} \right) \right\} ^{-\frac{3}{2}} = (r^2)^{-\frac{3}{2}} \left\{ 1-\frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2}+\frac{1}{4} \left(\frac{d}{r}\right)^2 \right\} ^{-\frac{3}{2}} \simeq r^{-3} \left\{ 1-\frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\} ^{-\frac{3}{2}} \simeq \frac{1}{r^3} \left\{ 1+\frac{3}{2} \frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\}
$$$$
\frac{1}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|^3}= \left\{ \left(\boldsymbol{r}+\frac{\boldsymbol{d}}{2}\right) \cdot \left(\boldsymbol{r}+\frac{\boldsymbol{d}}{2} \right) \right\} ^{-\frac{3}{2}} = (r^2)^{-\frac{3}{2}} \left\{ 1+\frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2}+\frac{1}{4} \left(\frac{d}{r}\right)^2 \right\} ^{-\frac{3}{2}} \simeq r^{-3} \left\{ 1+\frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\} ^{-\frac{3}{2}}\simeq \frac{1}{r^3} \left\{ 1-\frac{3}{2} \frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\}
$$これらを用いると、静電場の表式として以下が得られる。
$$
\boldsymbol{E}(\boldsymbol{r}) \simeq \boldsymbol{r} \left\{ \frac{q}{4\pi \epsilon_0} \frac{1}{r^3} \frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\} – \frac{\boldsymbol{d}}{2} \left\{ \frac{q}{4\pi \epsilon_0}\frac{2}{r^3} \right\} = \frac{1}{4\pi \epsilon_0} \left[ \frac{3(\boldsymbol{p}\cdot \boldsymbol{r})\boldsymbol{r}}{r^5}-\frac{\boldsymbol{p}}{r^3} \right]
$$□

＞＞別稿で議論しているように、ビオサバールの法則より、クーロンゲージ\(\nabla \cdot \boldsymbol{A} = 0\)を満たすベクトルポテンシャル\(\boldsymbol{A}(\boldsymbol{r})\)は以下で与えられる。
$$
\boldsymbol{A}(\boldsymbol{r}) = \frac{\mu_0 I}{4\pi} \oint_C \frac{d\boldsymbol{r’}}{|\boldsymbol{r} – \boldsymbol{r’}|}
$$回路のサイズに対して十分遠方にある観測点\(\boldsymbol{r}\)(ただし、回路上の位置を\(\boldsymbol{r’}\)としたとき、\(|\boldsymbol{r}| \gg |\boldsymbol{r’}|\)である)において、\(\frac{1}{|\boldsymbol{r} – \boldsymbol{r’}|})を(\boldsymbol{r’}\)について1次の項までテイラー展開すると、
$$
\frac{1}{|\boldsymbol{r} – \boldsymbol{r’}|} \approx \frac{1}{|\boldsymbol{r}|} + \boldsymbol{r’} \cdot \nabla’ \left( \frac{1}{|\boldsymbol{r} – \boldsymbol{r’}|} \right)_{\boldsymbol{r’}=0} = \frac{1}{r} + \frac{\boldsymbol{r} \cdot \boldsymbol{r’}}{r^3}
$$ただし\(r = |\boldsymbol{r}|\)としている。これをベクトルポテンシャルの式に代入すると、
$$
\boldsymbol{A}(\boldsymbol{r}) \approx \frac{\mu_0 I}{4\pi} \left[ \frac{1}{r} \oint_C d\boldsymbol{r’} + \frac{1}{r^3} \oint_C (\boldsymbol{r} \cdot \boldsymbol{r’}) d\boldsymbol{r’} \right]
$$第1項は、変位ベクトルの閉路積分であるため、始点と終点が一致し０になる。
第2項は、回路\(C\)が囲む面積を大きさとし、回路を含む平面に対して垂直で、電流の方向に右ねじを回して進む向きのベクトルを面積ベクトル\(\boldsymbol{S}\)としたとき、定ベクトル\(\boldsymbol{k}\)に対するベクトル解析の恒等式\(\oint_C (\boldsymbol{k} \cdot \boldsymbol{r’}) d\boldsymbol{r’} = \boldsymbol{S} \times \boldsymbol{k}\)を用いて変形すると、
$$
\oint_C (\boldsymbol{r} \cdot \boldsymbol{r’}) d\boldsymbol{r’} = \boldsymbol{S} \times \boldsymbol{r}
$$以上より、ベクトルポテンシャルは
$$
\boldsymbol{A}(\boldsymbol{r}) \approx \frac{\mu_0 I}{4\pi r^3} (\boldsymbol{S} \times \boldsymbol{r}) = \frac{\mu_0}{4\pi} \frac{\boldsymbol{m} \times \boldsymbol{r}}{r^3}
$$である。この回転を計算すると、以下が得られる。
$$
\boldsymbol{B}(\boldsymbol{r}) = \nabla \times \boldsymbol{A} = \frac{\mu_0}{4\pi} \left[ \frac{3(\boldsymbol{m} \cdot \boldsymbol{r})\boldsymbol{r}}{r^5} – \frac{\boldsymbol{m}}{r^3} \right]
$$□

３次元円筒座標系\((r,\theta,z)\)を設定し、それぞれが増加する方向の単位ベクトル\(\boldsymbol{e}_r,\boldsymbol{e}_\theta,\boldsymbol{e}_z\)とする。
観測点の位置を\(\boldsymbol{r}=(r, 0, 0)\)、電流素片の位置を\(\boldsymbol{r}’=(0, 0, z)\)としたとき、電流素片\(Idz \boldsymbol{e}_z\)が位置\(\boldsymbol{r}\)につくる磁場は、ビオサバールの法則より、
$$
\boldsymbol{B}(\boldsymbol{r}) = \frac{\mu_0 I}{4\pi} \int_{-\infty}^{\infty} \frac{dz \boldsymbol{e}_z \times (r \boldsymbol{e}_r – z \boldsymbol{e}_z)}{(r^2 + z^2)^{3/2}} = \frac{\mu_0 I}{4\pi} \int_{-\infty}^{\infty} \frac{r dz}{(r^2 + z^2)^{3/2}} \boldsymbol{e}_\theta
$$積分において\(z = r \tan \phi\)と置換すると、\(\int_{-\infty}^{\infty} \frac{r}{(r^2 + z^2)^{3/2}} dz = \frac{2}{r}\)となるため、以下が得られる。
$$
\boldsymbol{B}(\boldsymbol{r}) = \frac{\mu_0 I}{2\pi r} \boldsymbol{e}_\theta
$$□

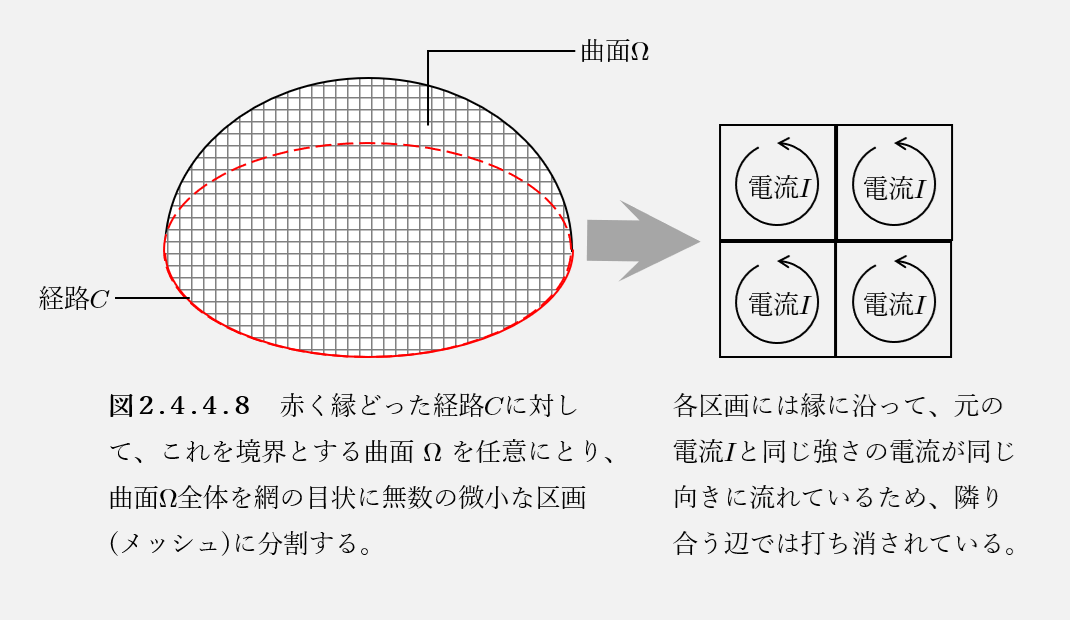
図２.４.４.８より、曲面内部のすべての境界線において、隣り合う微小回路の電流は互いに逆向きに流れるため、その効果は打ち消し合う。一方で、曲面\(\Omega\)の外縁(すなわち閉経路\(C\))に接する辺だけは打ち消す相手がいないため、電流\(I\)がそのまま残るので、現象的には、閉経路\(C\)を流れる一つの大きな電流と等価になる。□

任意の閉曲面\(S\)を、閉曲面を閉経路が貫かないようにとるとは、閉曲面が閉経路を完全に含む、もしくは閉局面が閉経路を完全に含まないのどちらかの状態ということである。このとき、閉経路\(C\)を縁(境界)として、閉曲面\(S\)と交わりをもたないような、曲面\(\Omega\)を仮想的に張ることができるため、閉経路\(C\)を流れる一つの大きな定常電流\(I\)は補題２.４.４.９より、このように張った曲面\(\Omega\)を埋め尽くす無数の電流ループの集合と等価といえる。
さて、曲面\(\Omega\)を埋め尽くすすべての電流ループは、その大きさに対して閉曲面\(S\)上のすべての点が十分遠方にあるとみなせるほど微小にとることができる。したがって、閉曲面\(S\)における、閉経路\(C\)を流れる定常電流\(I\)のつくる磁場の面積分は、補題２.４.４.６と補題２.４.４.７より、磁気双極子の集まりがつくる磁場の面積分とみなせる。
電気双極子とのアナロジーを考えると、閉曲面が電気双極子の集まりを完全に含む、もしくは完全に含まない、どちらの状態においても閉曲面内の電荷の合計は０であるから、電場におけるガウスの法則より、電気双極子の集まりがつくる電場の面積分は０である。よって、系２.４.４.10の仮定の下で、\(\oint_{S} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0\)が成立する。□

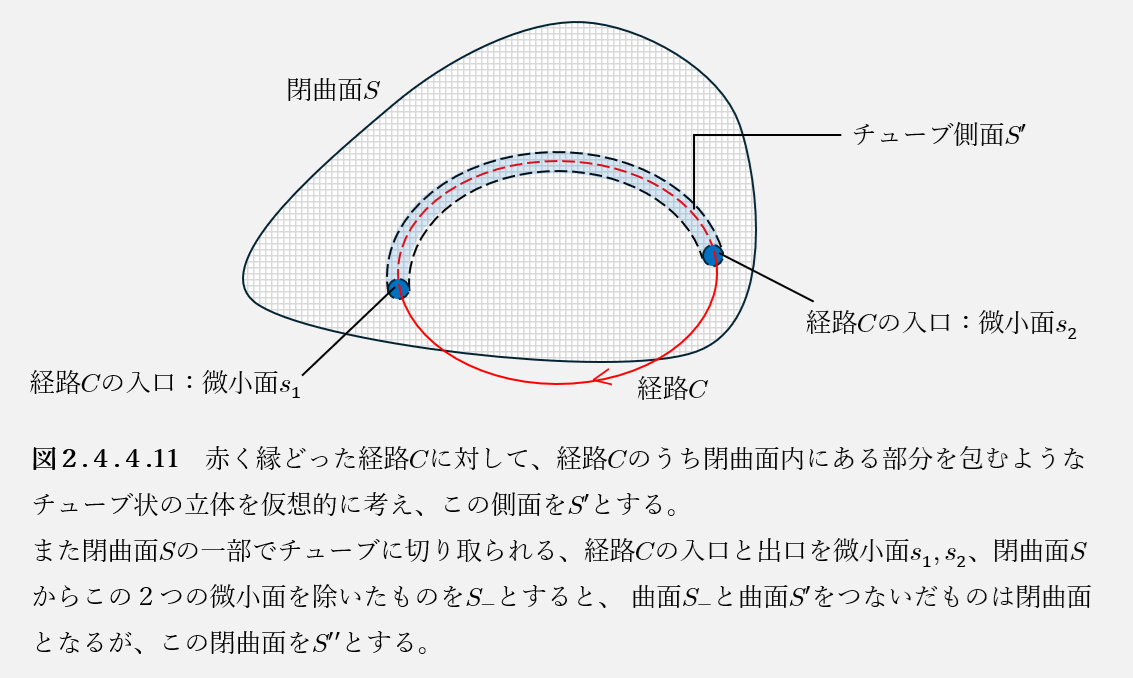
図２.４.４.11のように、閉経路\(C\)と閉曲面\(S\)に対して、曲面\(S’\)、微小面\(s_1,s_2\)、曲面\(S_{-}\)、閉曲面\(S”\)をとる。なおチューブは経路\(C\)を軸に等方的であるとする。
まずはじめに、チューブの半径は回路の大きさに比べて十分小さいため、このチューブ\(S’\)の表面近傍では、導線に流れる電流は無限に長い直線電流と近似することができ、回路の他の部分の影響は無視できるとみなせる。このとき補題２.４.４.８より、チューブ\(S’\)の表面において、磁場\(\boldsymbol{B}\)と法線方向の単位ベクトル\(\boldsymbol{n}\)は互いに垂直であるから、チューブ表面のあらゆる点においてその内積は０になる。したがって、以下が成り立つ。
$$
\int_{S’} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0
$$次に閉曲面\(S”\)について、この閉曲面は閉経路に貫かれていないので、系２.４.４.10より以下が成立する。
$$
\oint_{S”} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0
$$閉曲面\(S”\)は曲面\(S_{-}\)と曲面\(S′\)をつないだものであるから、その面積分について、
$$
\oint_{S”} \boldsymbol{B} \cdot \boldsymbol{n} dS = \int_{S_{-}} \boldsymbol{B} \cdot \boldsymbol{n} dS – \int_{S’} \boldsymbol{B} \cdot \boldsymbol{n} dS
$$が成立する。したがって、\(\int_{S’} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0\)と\(\oint_{S”} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0\)を代入すると、以下がわかる。
$$
\int_{S_{-}} \boldsymbol{B} \cdot \boldsymbol{n} dS \left( = \int_S \boldsymbol{B} \cdot \boldsymbol{n} dS – \int_{s_1} \boldsymbol{B} \cdot \boldsymbol{n} dS – \int_{s_2} \boldsymbol{B} \cdot \boldsymbol{n} dS \right) = 0
$$
最後に微小面\(s_1,s_2\)上での磁場の面積分を調べる。
面\(s_1,s_2\)は十分微小であるため、この微小面\(s_1,s_2\)上では、導線に流れる電流は無限に長い直線電流と近似することができ、回路の他の部分の影響は無視できるとみなせる。このとき補題２.４.４.８より、磁場\(\boldsymbol{B}\)の大きさは、導線からの距離\(r\)に反比例するから、\(C\)を定数として、\(|\boldsymbol{B}(\rho)| \approx \frac{C}{\rho}\)と扱える。
これをふまえて、微小面\(s_1,s_2\)の半径を\(\epsilon\)とすると、\(|\boldsymbol{B} \cdot \boldsymbol{n}| \leq |\boldsymbol{B}|\)より、微小面\(s_1,s_2\)における磁場の面積分の絶対値\(|\Phi_{\epsilon}|\)は、極座標\(\rho, \theta\)を用いて、以下のように評価できる。
$$
\left| \int_{s_i} \boldsymbol{B} \cdot \boldsymbol{n} dS \right| \leq \int_{s_i} |\boldsymbol{B}|dS \approx \int_{0}^{2\pi} \int_{0}^{\epsilon} \left( \frac{C}{\rho} \right) \cdot (\rho \, d\rho \, d\theta) = C \int_{0}^{2\pi} d\theta \int_{0}^{\epsilon} d\rho = 2\pi C \cdot \epsilon
$$これより、当該領域における磁場の面積分は、半径\(\epsilon\)の1乗のオーダーで振る舞うことがわかるので、チューブを無限に細くする極限\(\epsilon \to 0\)において、\(\int_{s_i} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0\)、つまり、以下が成立する。
$$
\oint_{S} \boldsymbol{B} \cdot \boldsymbol{n} dS = \int_{S_{-}} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0
$$□

定常電流場においては、電流線が途切れることなく連続しているので、任意の電流分布は、微小な電流 \(I_1\),\(I_2\),…,\(I_k\)…が流れる無数の閉じた閉経路\(C_1\),\(C_2\),…,\(C_k\)の集まりとして扱える。
このとき、\(I_1\),\(I_2\),…\(I_k\),…がそれぞれ単独で作る磁場を\(\boldsymbol{B}_1\),\(\boldsymbol{B}_2\),…\(\boldsymbol{B}_k\),…とすると、ある位置\(\boldsymbol{r}\)での磁場は、重ね合わせの原理より、
$$
\boldsymbol{B}(\boldsymbol{r}) = \sum_{k} \boldsymbol{B}_k(\boldsymbol{r})
$$と表せる。ここで、これまで示した２つの系より、閉経路\(C_k\)が閉曲面\(S\)を貫いていようがいまいが、\(\oint_{S} \boldsymbol{B}_k \cdot \boldsymbol{n} dS = 0\)であることから、閉曲面\(S\)に対して電場の面積分を計算すると、
$$
\displaystyle \int_{S} \boldsymbol{B}(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = \displaystyle \int_{S} \left(\sum_{k} \boldsymbol{B}_k(\boldsymbol{r})\right) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = \sum_{k} {\displaystyle \int_{S} \boldsymbol{B}_k(\boldsymbol{r}) \cdot \boldsymbol{n(\boldsymbol{r})} dS} = 0
$$となり、これより示された。□