静電場におけるガウスの法則

こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

静電場におけるガウスの法則は、各位置における電場の発散がその位置における電荷密度に比例するという法則で、静電場の基本法則の一つでもあります。

積分形のガウスの法則

積分形のガウスの法則
任意の閉曲面\(S\)をとり、また、\(\boldsymbol{n}(\boldsymbol{r})\)は閉曲面上の各位置\(\boldsymbol{r}\)での面を外向きに貫く大きさ1の法線ベクトルを、\(q\)は閉曲面内の電荷の総合計を表すこととする。このとき以下が成立する。
$$
\displaystyle \int_{S} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = \frac{q}{\epsilon_0}
$$

これを示すために補題としてまず以下のことを示します。

補題１
点電荷\(q\)のみ存在する空間において、任意の閉曲面\(S\)をこの点電荷を含むようにとり、また、\(\boldsymbol{n}(\boldsymbol{r})\)は閉曲面上の各位置\(\boldsymbol{r}\)での面を外向きに貫く大きさ1の法線ベクトルを表すこととする。このとき以下が成立する。
$$
\displaystyle \int_{S} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = \frac{q}{\epsilon_0}
$$

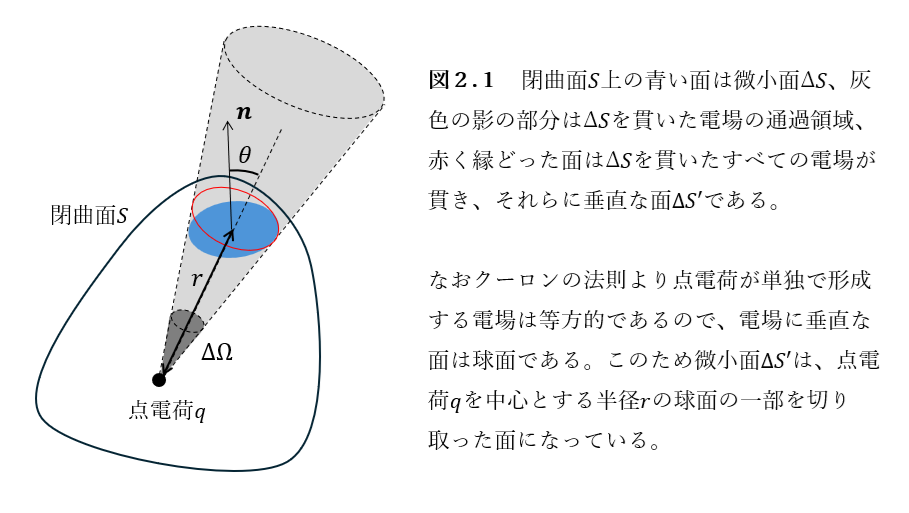
証明　任意の閉曲面\(S\)について、その閉曲面上での電場の面積分を計算する。図２より、\(\Delta S’=\Delta S \cos \theta\)であり、また立体角の定義から、半径\(r\)の球において立体角\(\Delta \Omega\)に対する曲面\(\Delta S’\)は、\(\Delta S’=r^2 \Delta \Omega\)と表せることをふまえると、
$$
\frac{r^2 \Delta \Omega}{\cos \theta}=\Delta S
$$とかける。これは、\(\Delta S\)が0に収束する極限でも成立するので、電場の面積分を計算すると、
$$
\displaystyle \int_{S} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = \displaystyle \int_{S} E(\boldsymbol{r}) n(\boldsymbol{r}) \cos \theta \frac{r^2 d\Omega}{\cos \theta} = \displaystyle \int_{S} E(\boldsymbol{r}) r^2 d\Omega = \frac{q}{4\pi \epsilon_0} \displaystyle \int_{S} d\Omega = \frac{q}{\epsilon_0}
$$となり、これより示された。□

これより直ちに次のことも成り立ちます。

補題2
点電荷\(q\)のみ存在する空間において、任意の閉曲面\(S\)をこの点電荷を含まないようにとり、また、\(\boldsymbol{n}(\boldsymbol{r})\)は閉曲面上の各位置\(\boldsymbol{r}\)での面を外向きに貫く大きさ1の法線ベクトルを表すこととします。このとき以下が成立します。
$$
\displaystyle \int_{S} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = 0
$$

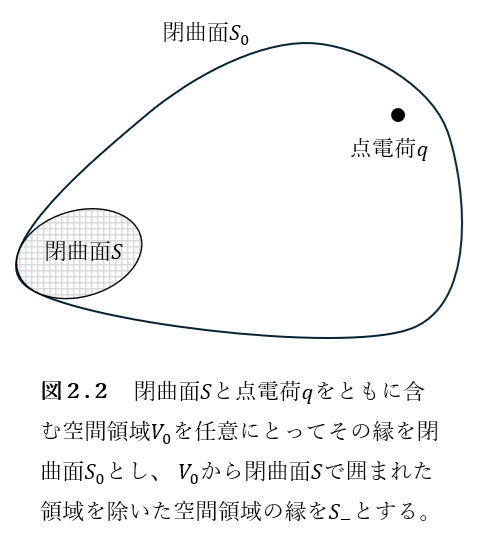
証明　任意の閉曲面\(S\)について、その閉曲面上での電場の面積分を計算する。図３のように閉曲面\(S_0\),\(S_{-}\)をとると、面積分の性質から、
$$
\displaystyle \int_{S} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = \displaystyle \int_{S_0} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS – \displaystyle \int_{S_{-}} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS
$$とかける。閉曲面\(S_0\),\(S_{-}\)はともに点電荷\(q\)を含んでいるので、先に示したことより、
$$
\displaystyle \int_{S_0} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = \displaystyle \int_{S_{-}} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = \frac{q}{\epsilon_0}
$$であるから、\(\displaystyle \int_{S} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = \frac{q}{\epsilon_0} – \frac{q}{\epsilon_0} = 0\)となり、これより示された。□

示す補題は以上です。これらから積分形のガウスの法則を示していきます。

証明　任意の電荷分布は点電荷の集まりとみなせるので、ある電荷分布について、これは閉曲面\(S\)内の点電荷\(q_1\),\(q_2\),…\(q_i\),…と閉曲面\(S\)外の点電荷\(Q_1\),\(Q_2\),…\(Q_j\),…の集まりとして扱える。このとき、\(q_1\),\(q_2\),…\(q_i\),…がそれぞれ単独で作る電場を\(\boldsymbol{e}_1\),\(\boldsymbol{e}_2\),…\(\boldsymbol{e}_i\),…とし、\(Q_1\),\(Q_2\),…\(Q_j\)がそれぞれ単独で作る電場を\(\boldsymbol{E}_1\),\(\boldsymbol{E}_2\),…\(\boldsymbol{E}_j\),…とすると、ある位置\(\boldsymbol{r}\)での電場は、
$$
\boldsymbol{E}(\boldsymbol{r}) = \sum_{i} \boldsymbol{e}_i(\boldsymbol{r}) + \sum_{j} \boldsymbol{E}_j(\boldsymbol{r})
$$と表せる。ここで、これまで示した２つの補題より、
$$
\displaystyle \int_{S} \boldsymbol{e}_i(\boldsymbol{r}) \cdot \boldsymbol{n(\boldsymbol{r})} dS = \frac{q_i}{\epsilon_0}
$$$$
\displaystyle \int_{S} \boldsymbol{E}_i(\boldsymbol{r}) \cdot \boldsymbol{n(\boldsymbol{r})} dS = 0
$$であることから、閉曲面\(S\)に対して電場の面積分を計算すると、
$$
\displaystyle \int_{S} \boldsymbol{E}(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = \displaystyle \int_{S} \left(\sum_{i} \boldsymbol{e}_i(\boldsymbol{r}) + \sum_{j} \boldsymbol{E}_j(\boldsymbol{r})\right) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = \left(\sum_{i} {\displaystyle \int_{S} \boldsymbol{e}_i(\boldsymbol{r}) \cdot \boldsymbol{n(\boldsymbol{r})} dS}\right) + \left(\sum_{j} {\displaystyle \int_{S} \boldsymbol{E}_j(\boldsymbol{r}) \cdot \boldsymbol{n(\boldsymbol{r})} dS}\right) = \frac{\sum_i q_i}{\epsilon_0}
$$となり、これより示された。□

微分形のガウスの法則

物理学の理論が進んでいくにつれ、遠く離れた場所が直接作用しあうのではなく、隣へ隣へと作用が通じて伝わっていくという見方が、より正確な理解を助けることがわかってきました。このすぐ隣同士の局所的な因果関係を記述するものは、積分形に対して微分形と呼ばれることが多いです。
いま紹介したガウスの法則の記述は、ある空間領域全体での電場の発散がその空間領域全体での電荷に比例することを主張したもので、これに対して局所的な位置での主張を記述した式は、微分形のガウスの法則といいます。

微分形のガウスの法則
以下のように記述する。ただし、\(\rho(\boldsymbol{r})\)は各位置\(\boldsymbol{r}\)での電荷密度を表す。
$$
\nabla \cdot \boldsymbol{E}(\boldsymbol{r}) = \frac{\rho(\mathbf{r})}{\epsilon_0}
$$

証明　ある閉曲面を\(S\)をとり、その閉曲面内の空間領域を\(V\)とする。このとき、積分形のガウスの法則より、
$$
\displaystyle \int_{S} \boldsymbol{E(\boldsymbol{r})} \cdot \boldsymbol{n(\boldsymbol{r})} dS = \frac{q}{\epsilon_0}
$$が成り立つ。ここで、左辺はガウスの発散定理より、
$$
\displaystyle \int_S \boldsymbol{E} (\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = \displaystyle \int_V \nabla \cdot \boldsymbol{E} (\boldsymbol{r}) dV
$$と変形でき、右辺はある空間領域内での電荷の総合計は、その空間領域内で電荷密度を体積分した表式で与えられることから、
$$
q= \displaystyle \int_V \rho(\boldsymbol{r}) dV
$$と変形できるので、積分形の電荷の保存則は、
$$
\displaystyle \int_V \nabla \cdot \boldsymbol{E} (\boldsymbol{r}) dV = \displaystyle \int_V \frac{\rho(\boldsymbol{r})}{\epsilon_0} dV
$$と書き換えられることがわかる。いま、空間領域\(V\)は任意にとれるので、この関係がつねに成り立つには、
$$
\nabla \cdot \boldsymbol{E}(\boldsymbol{r})= \frac{\rho(\boldsymbol{r})}{\epsilon_0}
$$でなくてはならない。これははじめに与えた表式であるので、これより示された。□

以上、静電場におけるガウスの法則の積分形および微分形の記述と、その証明になります。