磁性体における境界条件

こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

親記事で、マクロに見たとき磁場をかけるとそれにしたがって磁気双極子モーメントが現れるという性質を持つ磁性体について、それをよく説明するモデルを用いて磁性体における静磁場の満たす法則を導きました。本稿では、これらを用いて、磁性体の境界条件や磁性体における静磁場を決定する方法について考えていきます。
なお、前回すでに与えている定理２.４.Ｍ(物質中のマクスウェル方程式)について、本稿では静電場や静磁場を扱うので、ここで時間変化のしない物質中のマクスウェル方程式の微分形および積分形を与えておきます。積分形と微分形が等価である証明は、定理２.４.３とよく似ているので省略します。

定理２.４.Ｍ.１(物質中の時間変化しないマクスウェル方程式)
誘電体をプラスとマイナスのシートが重なり合ったモデルとみなし、磁性体を微小な電流ループが敷き詰められているモデルとみなしたとき、物質中の電場$\boldsymbol{E}$、磁場$\boldsymbol{B}$に対し、電束密度$\boldsymbol{D}$を$\boldsymbol{D} = \epsilon_0 \boldsymbol{E} + \boldsymbol{P}$、磁場の強さ$\boldsymbol{H}$を$\boldsymbol{H} = \frac{1}{\mu_0}\boldsymbol{B} – \boldsymbol{M}$と定義すると、以下が成立する。
$$
\nabla \cdot \boldsymbol{D} = \rho_f
$$$$
\nabla \cdot \boldsymbol{B} = 0
$$$$
\nabla \times \boldsymbol{E} = \boldsymbol{0}
$$$$
\nabla \times \boldsymbol{H} = \boldsymbol{j}_f
$$ただし、$\epsilon_0$は真空の誘電率、$\mu_0$は真空の透磁率、$\rho_f$は真電荷密度、$\boldsymbol{j}_f$は真電流密度、分極ベクトル$\boldsymbol{P}$は電気双極子モーメントの密度、磁化ベクトル$\boldsymbol{M}$は磁気双極子モーメントの密度である。

定理２.４.Ｍ.２(物質中の時間変化しない積分形のマクスウェル方程式)
誘電体をプラスとマイナスのシートが重なり合ったモデルとみなし、磁性体を微小な電流ループが敷き詰められているモデルとみなしたとき、物質中の電場$\boldsymbol{E}$、磁場$\boldsymbol{B}$に対し、電束密度$\boldsymbol{D}$を$\boldsymbol{D} = \epsilon_0 \boldsymbol{E} + \boldsymbol{P}$、磁場の強さ$\boldsymbol{H}$を$\boldsymbol{H} = \frac{1}{\mu_0}\boldsymbol{B} – \boldsymbol{M}$と定義すると、以下が成立する。

(1) 電場におけるガウスの法則(積分形)
任意の閉曲面$S$に対し、その閉曲面内部に含まれる真電荷の合計を$Q_f$とすると、
$$
\oint_{S} \boldsymbol{D} \cdot \boldsymbol{n} dS = Q_f
$$(2) 磁場におけるガウスの法則(積分形)
任意の閉曲面$S$に対して、
$$
\oint_{S} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0
$$(3) ファラデーの電磁誘導の法則(積分形)
任意の閉曲線$C$について、その閉曲線を縁とする任意の曲面を$S$とすると、
$$
\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r} = 0
$$(4) アンペール-マクスウェルの法則(積分形)
任意の閉曲線$C$について、その閉曲線を縁とする任意の曲面を$S$として、その曲面を通過する全真電流の、閉曲線$C$の向きに右ねじを回して進む向きを正とした合計を$I_f$とすると、
$$
\oint_{C} \boldsymbol{H} \cdot d\boldsymbol{r} = \mu_0 I_f
$$ただし、$\epsilon_0$は真空の誘電率、$\mu_0$は真空の透磁率、分極ベクトル$\boldsymbol{P}$は電気双極子モーメントの密度、磁化ベクトル$\boldsymbol{M}$は磁気双極子モーメントの密度である。

磁性体の境界条件と静電場

本稿ではとくに、磁化ベクトル$\boldsymbol{M}$と磁場$\boldsymbol{B}$の向きが一致する場合を扱います。一般に多くの状況でこれがあてはまり、このとき定義２.４.Ｌのようにして磁性体に透磁率$\mu$を定義できます。

透磁率一様の領域での静磁場

ある有限あるいは無限の領域$V$について、この領域の透磁率が$\mu$で一様であり、さらに領域$V$の外部との境界を除くすべての位置$\boldsymbol{r}$における真電流分布$\boldsymbol{j}_f(\boldsymbol{r})$が与えられたとします。このとき、領域$V$内部の静磁場を求めることを考えてみましょう。
定理２.４.Ｍ.１と定義２.４.Ｌより、静磁場について$\nabla \times \boldsymbol{B} = \mu \boldsymbol{j}_f$, $\nabla \cdot \boldsymbol{B} = \boldsymbol{0}$の２式が成り立つことになります。ここで第２式より、クーロンゲージ条件$\nabla \cdot \boldsymbol{A}=0$を満たす$\boldsymbol{B} = \nabla \times \boldsymbol{A}$なるベクトル場$\boldsymbol{A}$を定義することができるので、これを第１式に代入すると、以下が成立しますね。
$$
-\nabla^2 \boldsymbol{A}(\boldsymbol{r}) = \mu \boldsymbol{j}_f(\boldsymbol{r})
$$これは、別稿で扱った真空におけるポアソン方程式の$\mu_0$を$\mu$に置き換えたものであるので、境界条件として、領域$V$が有限であるときは(1)から(3)、領域$V$が無限(縁がない全空間)であるときは(4)のような条件が与えられれば、解を一意に定めることができます。

(1)ディリクレ条件：境界上のすべての場所での、ベクトルポテンシャル$\boldsymbol{A}$を与える条件
領域$V$の表面$S$上のある位置$\boldsymbol{r}$におけるベクトルポテンシャル$\boldsymbol{A}$の関数形$\boldsymbol{f}(\boldsymbol{r})$が与えられる条件です。

(2)ノイマン条件：境界上のすべての場所での、ベクトルポテンシャル$\boldsymbol{A}$の法線方向微分を与える条件
領域$V$の表面$S$上のある位置$\boldsymbol{r}$におけるベクトルポテンシャルの法線方向微分$\frac{\partial \boldsymbol{A}}{\partial n}$の関数形$\boldsymbol{g}(\boldsymbol{r})$が与えられる条件です。
このノイマン条件については、ベクトルポテンシャル$\boldsymbol{A}$には定ベクトル分のずれが残ります($\boldsymbol{A}$が解であるとすると、定ベクトル$\boldsymbol{\chi}$に対して$\boldsymbol{A}+\boldsymbol{\chi}$も解になります)。物理的には磁場のみが意味を持つのでこれで問題ないですが、ベクトルポテンシャル$\boldsymbol{A}$の関数形まで確定させたい場合には、領域$V$中のあるどこか１点$\boldsymbol{r}_0$でのベクトルポテンシャルの値$\boldsymbol{A}(\boldsymbol{r}_0)$を与える必要があります。

(3)混合境界条件：境界の一部ではベクトルポテンシャル$\boldsymbol{A}$を、残りの部分ではベクトルポテンシャル$\boldsymbol{A}$の法線方向微分を与える条件
境界$S$を2つの部分$S_1$と$S_2$に分け、$S_1$上では$\boldsymbol{A}$の関数形が、$S_2$上では $\frac{\partial \boldsymbol{A}}{\partial n}$の関数形が与えられる条件です。

(4)無限遠での条件：無限遠でベクトルポテンシャル$\boldsymbol{A}$が漸近する関数形を与える条件
$|\boldsymbol{r}| \to \infty$で$\boldsymbol{A}(\boldsymbol{r}) \to \boldsymbol{A}_{\text{ext}}(\boldsymbol{r})$なる関数形$\boldsymbol{A}_{\text{ext}}(\boldsymbol{r})$を与える条件です(例えば、電流がある有限の領域に集まっているときは、無限遠でのベクトルポテンシャルは$\boldsymbol{0}$に収束します)。

透磁率の異なる複数領域での静磁場

ある有限あるいは無限の領域$V$についてこの領域が、透磁率が$\mu_1$で一様な$V_1$と、誘電率が$\mu_2$で一様な$V_2$の２つに分けられ、さらに領域$V$の外部との境界および、領域$V_1$と$V_2$の境界を除くすべての位置$\boldsymbol{r}$における真電流密度$\boldsymbol{j}_f(\boldsymbol{r})$が与えられたとします。このとき、領域$V$内部の静磁場を求めることを考えましょう。
先と同様に、定理２.４.Ｍ.１と定義２.４.Ｌより、以下が成り立ちます。
$$
-\nabla^2 \boldsymbol{A}(\boldsymbol{r}) = \mu_1 \boldsymbol{j}_f(\boldsymbol{r}) \quad (\boldsymbol{r} \in V_1)
$$$$
-\nabla^2 \boldsymbol{A}(\boldsymbol{r}) = \mu_2 \boldsymbol{j}_f(\boldsymbol{r}) \quad (\boldsymbol{r} \in V_2)
$$この場合は、領域$V$の境界条件として、領域$V$が有限であるときは先に挙げた(1)から(3)、領域$V$が無限(縁がない全空間)であるときは先に挙げた(4)のような条件が与えられるだけでは解が一意に定まらず、これに加えて、$V_1$と$V_2$の境界における以下の条件が必要です。

定理２.４.Ｍ.５
異なる磁性体１と２の境界面上の点$\boldsymbol{r}$における、誘電体２から１へ向かう方向の境界面に垂直な単位ベクトルを$\boldsymbol{n}(\boldsymbol{r})$、境界面に接する単位ベクトルを$\boldsymbol{t}(\boldsymbol{r})$、境界面上の真電流密度を$\boldsymbol{k}_f(\boldsymbol{r})$とする。このとき、点$\boldsymbol{r}$近傍の誘電体１側の磁場の強さ$\boldsymbol{H}_1(\boldsymbol{r})$、静磁場$\boldsymbol{B}_1(\boldsymbol{r})$、誘電体２側の磁場の強さ$\boldsymbol{H}_2(\boldsymbol{r})$、静磁場$\boldsymbol{B}_2(\boldsymbol{r})$に対して、以下が成立する。
$$
\boldsymbol{B}_1(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) – \boldsymbol{B}_2(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) = 0
$$$$
\boldsymbol{H}_1(\boldsymbol{r}) \cdot \boldsymbol{t}(\boldsymbol{r}) – \boldsymbol{H}_2(\boldsymbol{r}) \cdot \boldsymbol{t}(\boldsymbol{r}) = \boldsymbol{k}_f(\boldsymbol{r}) \cdot \left( \boldsymbol{n}(\boldsymbol{r}) \times \boldsymbol{t}(\boldsymbol{r}) \right)
$$

定理２.４.Ｍ.５の証明

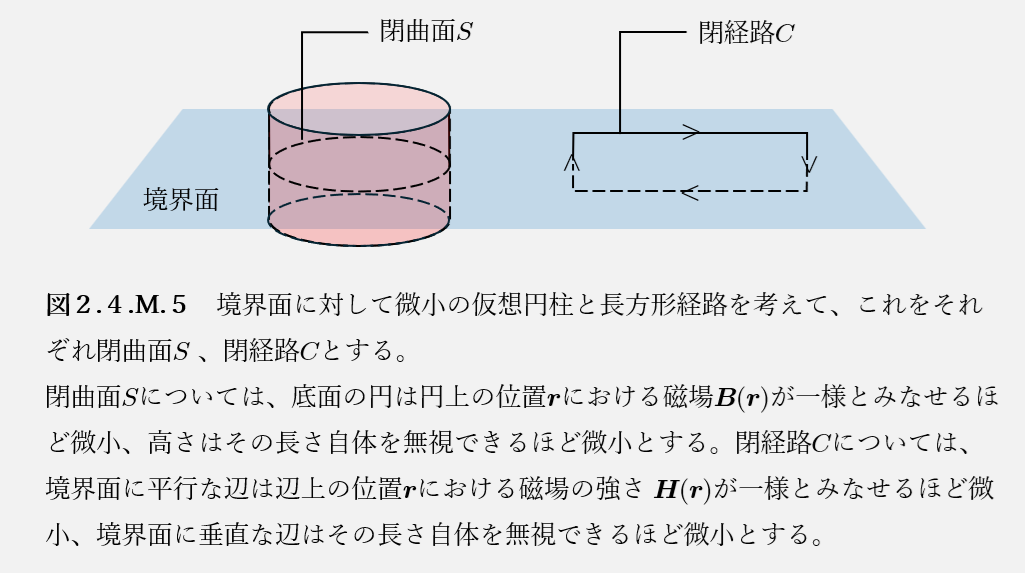
図２.４.Ｍ.５のように、境界面に対して微小の仮想の円柱と長方形経路を考えて、これをそれぞれ閉曲面$S$、閉経路$C$とすると、定理２.４.Ｍ.２(物質中の時間変化しない積分形のマクスウェル方程式)の第２式、第４式より、
$$
\oint_{S} \boldsymbol{B} \cdot \boldsymbol{n} dS = 0
$$$$
\oint_{C} \boldsymbol{H} \cdot d\boldsymbol{r} = \mu_0 I_f
$$が成立する。ただし、$I_f$はその閉曲線を縁とする面を通過する全真電流の、閉曲線$C$の向きに右ねじを回して進む向きを正とした合計である。
閉曲面$S$について、底面の円は円上の位置$\boldsymbol{r}$における磁場$\boldsymbol{B}(\boldsymbol{r})$が一様とみなせるほど微小、高さはその長さ自体を無視できるほど微小であるので、底面の円の面積を$\Delta S$とすると、第１式の左辺は円柱側面からの寄与を０とみなして、$\oint_{S} \boldsymbol{B} \cdot \boldsymbol{n} dS = \left\{ \boldsymbol{B}_1(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) – \boldsymbol{B}_2(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) \right\} \Delta S$とかける。右辺は０であるので、以下が得られる。
$$
\boldsymbol{D}_1(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) – \boldsymbol{D}_2(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) = 0
$$閉経路$C$について、境界面に平行な辺は辺上の位置$\boldsymbol{r}$における磁場の強さ$\boldsymbol{H}(\boldsymbol{r})$が一様とみなせるほど微小、高さはその長さ自体を無視できるほど微小であるので、境界面に平行な辺の長さを$\Delta l$とすると、第３式の左辺は境界面に垂直な辺からの寄与を０とみなして、$\oint_{C} \boldsymbol{H} \cdot d\boldsymbol{r} = \left\{ \boldsymbol{H}_1(\boldsymbol{r}) \cdot \boldsymbol{t}(\boldsymbol{r}) – \boldsymbol{H}_2(\boldsymbol{r}) \cdot \boldsymbol{t}(\boldsymbol{r}) \right\} \Delta l$とかける。右辺は$I_f=\boldsymbol{k}_f(\boldsymbol{r}) \cdot \left( \boldsymbol{n}(\boldsymbol{r}) \times \boldsymbol{t}(\boldsymbol{r}) \right)$であるため、以下が得られる。
$$
\boldsymbol{H}_1(\boldsymbol{r}) \cdot \boldsymbol{t}(\boldsymbol{r}) – \boldsymbol{H}_2(\boldsymbol{r}) \cdot \boldsymbol{t}(\boldsymbol{r}) = \boldsymbol{k}_f(\boldsymbol{r}) \cdot \left( \boldsymbol{n}(\boldsymbol{r}) \times \boldsymbol{t}(\boldsymbol{r}) \right)
$$□

ここで、ある有限あるいは無限の領域$V$についてこの領域が、透磁率が$\mu_1$で一様な$V_1$と、透磁率が$\mu_2$で一様な$V_2$の２つに分けられ、さらに領域$V$の外部との境界および、領域$V_1$と$V_2$の境界を除くすべての位置$\boldsymbol{r}$における真電流密度$\boldsymbol{j}_f(\boldsymbol{r})$が与えられたとするとき、領域$V$の境界条件(領域$V$が有限であるときは先に挙げた(1)から(3)、領域$V$が無限(縁がない全空間)であるときは先に挙げた(4)のような条件)と、定理２.４.Ｍ.５の条件が満たされるような解は一意に定まります。
証明は、磁場におけるポアソン方程式の各成分は、数学的には電場におけるポアソン方程式と等しい構造になっていることから、各成分についてグリーンの第一恒等式に条件を代入する形で構成できますが、内容が煩雑であるため省略します。

この解の一意性から、次のことが直ちにいえますね。

系２.４.Ｍ.６
ある有限あるいは無限の領域$V$についてこの領域が、透磁率が$\mu_1$で一様な$V_1$と、透磁率が$\mu_2$で一様な$V_2$の２つに分けられ、領域$V$の外部との境界および、領域$V_1$と$V_2$の境界を除くすべての位置$\boldsymbol{r}$における真電流密度$\boldsymbol{j}_f(\boldsymbol{r})$、境界面上の真電流密度$\boldsymbol{k}_f(\boldsymbol{r})$が与えられているとする。
ここで、ある透磁率分布$\mu_a(\boldsymbol{r})$と真電流密度$\boldsymbol{j}_a(\boldsymbol{r})$に対して求められる磁場の強さ$\boldsymbol{H}_1(\boldsymbol{r})$、静磁場$\boldsymbol{B}_1(\boldsymbol{r})$、クーロンゲージを満たすベクトルポテンシャル$\boldsymbol{A}_1(\boldsymbol{r})$について、領域$V_1$においてもとと同じポアソン方程式
$$
-\nabla^2 \boldsymbol{A}_1(\boldsymbol{r}) = \mu_1 \boldsymbol{j}_f(\boldsymbol{r}) \quad (\boldsymbol{r} \in V_1)
$$を満たし、かつ領域$V$の外部との境界条件(領域$V$が有限であるときはディリクレ条件、ノイマン条件、混合境界条件のどれか、領域$V$が無限(縁がない全空間)であるときは無限遠での$\boldsymbol{A}$の関数形を与える条件)を満たすとする。
同様に、ある透磁率分布$\mu_b(\boldsymbol{r})$と真電流密度$\boldsymbol{j}_b(\boldsymbol{r})$に対して求められる磁場の強さ$\boldsymbol{H}_2(\boldsymbol{r})$、静磁場$\boldsymbol{B}_2(\boldsymbol{r})$、クーロンゲージを満たすベクトルポテンシャル$\boldsymbol{A}_2(\boldsymbol{r})$について、領域$V_2$においてもとと同じポアソン方程式
$$
-\nabla^2 \boldsymbol{A}_2(\boldsymbol{r}) = \mu_2 \boldsymbol{j}_f(\boldsymbol{r}) \quad (\boldsymbol{r} \in V_2)
$$を満たし、かつ領域$V$の外部との境界条件(領域$V$が有限であるときはディリクレ条件、ノイマン条件、混合境界条件のどれか、領域$V$が無限(縁がない全空間)であるときは無限遠での$\boldsymbol{A}$の関数形を与える条件)を満たすとする。このときこれらが、
$$
\boldsymbol{B}_1(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) – \boldsymbol{B}_2(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) = 0
$$$$
\boldsymbol{H}_1(\boldsymbol{r}) \cdot \boldsymbol{t}(\boldsymbol{r}) – \boldsymbol{H}_2(\boldsymbol{r}) \cdot \boldsymbol{t}(\boldsymbol{r}) = \boldsymbol{k}_f(\boldsymbol{r}) \cdot \left( \boldsymbol{n}(\boldsymbol{r}) \times \boldsymbol{t}(\boldsymbol{r}) \right)
$$を満足するならば、それが領域$V$内の静磁場$\boldsymbol{B}(\boldsymbol{r})$に他ならない。

これは、静磁場を求めるときに使う方法の一つである鏡像法などの裏付けになるため、実際に静磁場を求めるにあたって欠かせない内容になります。