導体における境界条件

こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

親記事で、導体においてはその内部のあらゆる位置\(\boldsymbol{r}\)において、静電場\(\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}\)となることを話しました。空間に電荷分布をつくるとき、考えている領域に導体があると、導体内部の自由電子が静電場を打ち消すように動くことで表面に電荷が現れ、これが外部電場に影響を与えます。
本稿ではこのような、考えている領域に導体があるときの、静電場や導体表面の面電荷を求める方法を見ていきます。

導体の境界条件と静電場

ある有限あるいは無限の領域\(V\)についてこの領域が、真空領域\(V_1\)と、導体領域\(V_2\)の２つに分けられ、さらに領域\(V_1\)と\(V_2\)の境界を除く、真空領域\(V_1\)内部のすべての位置\(\boldsymbol{r}\)における、電荷密度\(\rho(\boldsymbol{r})\)が与えられたとします。このとき、真空領域\(V_1\)内部の静電場および、領域\(V_1\)と\(V_2\)の境界における面電荷密度\(\sigma(\boldsymbol{r})\)を求めることを考えましょう。

定理２.４.Ａで確認したように、導体内部のあらゆる位置\(\boldsymbol{r}\)において、電位\(\phi(\boldsymbol{r})\)は一定でした。
これをふまえて先に結論から言うと、導体の電位が与えられ、かつ\(V_1\)の外部との境界条件(領域\(V_1\)が有限であるときは以下の(1)から(3)、領域\(V\)が無限(縁がない全空間)であるときは以下の(4)のような条件)が与えられれば、真空領域\(V_1\)内部の静電場\(\boldsymbol{E}(\boldsymbol{r})\)や電位\(\phi(\boldsymbol{r})\)は一意に定まります。

(1)ディリクレ条件：境界上のすべての場所での、スカラーポテンシャル\(\phi\)の値を与える条件
領域\(V\)の表面\(S\)上のある位置\(\boldsymbol{r}\)におけるスカラーポテンシャル\(\phi(\boldsymbol{r})\)の関数形\(f(\boldsymbol{r})\)が与えられる条件です。

(2)ノイマン条件：境界上のすべての場所での、スカラーポテンシャル\(\phi\)の法線方向微分の値を与える条件
領域\(V\)の表面\(S\)上のある位置\(\boldsymbol{r}\)におけるスカラーポテンシャルの法線方向微分\(\frac{\partial \phi}{\partial n}\)の関数形\(g(\boldsymbol{r})\)が与えられる条件です。
このノイマン条件については、スカラーポテンシャル\(\phi\)の値には定数差分のずれが残ります(\(\phi\)が解であるとすると、定数\(C\)に対して\(\phi+C\)も解になります)。物理的にはスカラーポテンシャルの差(電位差)、あるいは電場のみが意味を持つのでこれで問題ないですが、スカラーポテンシャル\(\phi\)の関数形まで確定させたい場合には、領域\(V\)中のあるどこか１点\(\boldsymbol{r}_0\)でのスカラーポテンシャルの値\(\phi(\boldsymbol{r}_0)\)を与える必要があります。

(3)混合境界条件：境界の一部ではスカラーポテンシャル\(\phi\)の値を、残りの部分ではスカラーポテンシャル\(\phi\)の法線方向微分の値を与える条件
境界\(S\)を2つの部分\(S_1\)と\(S_2\)に分け、\(S_1\)上では\(\phi\)の関数形が、\(S_2\)上では \(\frac{\partial \phi}{\partial n}\)の関数形が与えられる条件です。
現実的な実験系ではこれが最も一般的です(例えば、境界の一部は電圧をつないだ金属板、残りの部分は空気中に開放されているときは、金属板部分では\(\phi\)の関数形が、残りの部分では \(\frac{\partial \phi}{\partial n}\)の関数形が与えやすいですね)。

(4)無限遠での条件：無限遠でスカラーポテンシャル\(\phi\)が漸近する関数形を与える条件
\(|\boldsymbol{r}| \to \infty\)で\(\phi(\boldsymbol{r}) \to \phi_{\text{ext}}(\boldsymbol{r})\)なる関数形\(\phi_{\text{ext}}(\boldsymbol{r})\)を与える条件です(例えば、電荷がある有限の領域に集まっているときは、無限遠でのスカラーポテンシャルの値は０に収束します)。

導体の電位が与えられるということは、真空領域\(V_1\)と導体領域\(V_2\)の境界における電位の値\(\phi(\boldsymbol{r})\)が与えられているということなので、実は、真空領域\(V_1\)内部の静電場\(\boldsymbol{E}(\boldsymbol{r})\)や電位\(\phi(\boldsymbol{r})\)が一意に定まるということ自体は定理２.４.５.４、定理２.４.５.５、定理２.４.５.６、定理２.４.５.７の主張に含まれています。このため証明は省略します。

以上の境界条件が与えられると、理論的には、真空領域\(V_1\)内部の静電場が求まります。このとき、領域\(V_1\)と\(V_2\)の境界における面電荷密度\(\sigma(\boldsymbol{r})\)を次のように求めることができます。

定理２.４.Ｂ.１
導体表面における静電場を\(\boldsymbol{E}(\boldsymbol{r})\)とするとき、面電荷密度\(\sigma(\boldsymbol{r})\)について、\(\sigma(\boldsymbol{r})=\epsilon_0 |\boldsymbol{E}(\boldsymbol{r})\)|

定理２.４.Ｂ.１の証明

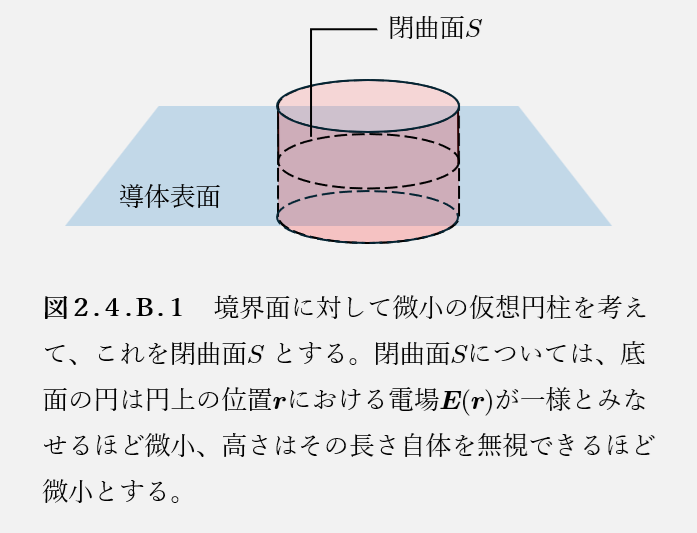
図２.４.Ｂ.１のように、境界面に対して微小の仮想の円柱を考えて、これを閉曲面\(S\)とすると、積分形のガウスの法則より、
$$
\oint_{S} \boldsymbol{E} \cdot \boldsymbol{n} dS = Q
$$が成立する。ただし、\(Q\)はその閉曲面内部に含まれる電荷の合計である。定理２.４.Ａより、導体内部のあらゆる位置\(\boldsymbol{r}\)において、静電場\(\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}\)であるので、電場の面積分の導体側にある面全体からの寄与は０である。また、定理２.４.Ｂより、導体表面における電場は\(\boldsymbol{0}\)もしくは導体表面に垂直であるので、真空領域側にある円柱底面で\(\boldsymbol{E} \cdot \boldsymbol{n} = |\boldsymbol{E}|\)とかけ、電場の面積分の側面全体からの寄与は\(\boldsymbol{E} \perp \boldsymbol{n}\)のため０である。以上をふまえると、左辺は、\(\oint_{S} \boldsymbol{E} \cdot \boldsymbol{n} dS = \boldsymbol{E}(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) \Delta S = |\boldsymbol{E}(\boldsymbol{r})| \Delta S\)とかける。右辺は\(\sigma(\boldsymbol{r}) \Delta S \)とかけるので、\(\Delta S\)で約分して以下が得られる。
$$
\sigma(\boldsymbol{r})=\epsilon_0 |\boldsymbol{E}(\boldsymbol{r})|
$$□

以上、導体と接する真空領域\(V_1\)内部の静電場および、領域\(V_1\)と\(V_2\)の境界における面電荷密度\(\sigma(\boldsymbol{r})\)の、理論上の求め方である。