こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。
電荷の保存則は孤立した系(外部との電荷の出入りがない閉じた空間)の内部では、正電荷と負電荷の総量が時間によって変化しないという法則です。エネルギー保存則や運動量保存則と並ぶ物理学における重要な保存則で、物理で議論する電荷に関するすべての現象がこの法則の制約のもとに成り立っています。本稿では、この保存則の数学的な記述を考えます。
積分形の電荷の保存則
法則1.1(積分形の電荷の保存則)
数学的には以下のように記述する。ただし、\(\boldsymbol{j}(\boldsymbol{r})\)は各位置\(\boldsymbol{r}\)での電流密度を、\(\boldsymbol{n}(\boldsymbol{r})\)は閉曲面上の各位置\(\boldsymbol{r}\)での面を外向きに貫く大きさ1の法線ベクトルを、\(q\)は閉曲面内の電荷の総合計を表す。
$$
\displaystyle \int_S \boldsymbol{j} (\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = -\frac{\partial q}{\partial t}
$$
証明 閉曲面\(S\)上の微小面\(\Delta S\)について、この微小面を通過する電流の合計の絶対値\(\Delta I\)は、\(\Delta S\)が微小面であるのでどこでも電流の向きは同じであるとみなすと、電流密度の定義より、
$$
\Delta I \simeq \text{|(微小面\(\Delta S\)における電流密度)×(\(\Delta S\)を貫く電流がすべて貫き、かつ電流に垂直な平面の面積)|}
$$とかける。
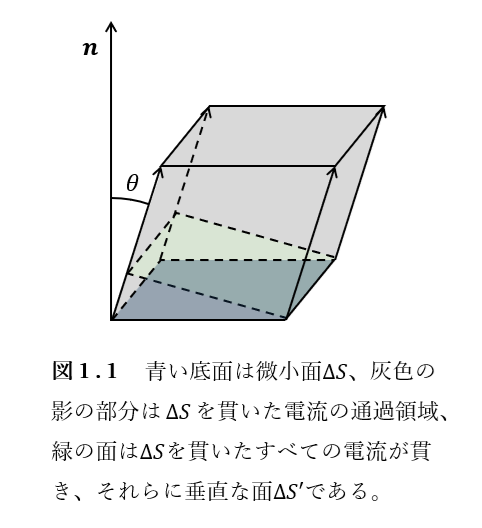
ここで、図1より、
$$
\text{(微小面\(\Delta S\)を貫く電流がすべて貫き、かつ電流に垂直な平面の面積)}=\text{\(\Delta S’\)の面積}=\Delta S \cos \theta
$$であるので、
$$
\Delta I \simeq j \Delta S \cos \theta = |\boldsymbol{j} \cdot \boldsymbol{n}| \Delta S
$$電流の大きさは単位時間あたりに通過する電荷量で定義されていることをふまえると、微小時間(\Delta t)において微小面\(\Delta S\)を通過する電荷の合計は、\(\Delta I \Delta t\)に等しいとみなせる。ここで、\(\Delta S\)が0に収束する極限を考えると、\(\Delta I\)を閉曲面\(S\)全体で足し合わせた結果は面積分の表式で与えられるので、微小時間\(\Delta t\)において閉曲面\(S\)から外側へ出ていく電荷の合計\(\Delta Q\)は、
$$
\Delta Q \simeq \left( \displaystyle \int_S \boldsymbol{j}(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS \right) \Delta t
$$ここで、電荷の保存則の主張とは、孤立した系の内部で電荷の総量が時間変化しないというものであったことを思い出すと、微小時間\(\Delta t\)で閉曲面内の電荷の総合計が符号付きで\(\Delta q\)変化したとき、\(\Delta q+\Delta Q=0\)を満足している必要があるので、
$$
\Delta q+ \left( \displaystyle \int_S \boldsymbol{j}(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS \right) \Delta t \simeq 0
$$両辺\(\Delta t\)で割ると、
$$
\displaystyle \int_S \boldsymbol{j}(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS \simeq -\frac{\Delta q}{\Delta t}
$$\(\Delta t\)が0に収束する極限で、この式の等号は成立するので、
$$
\displaystyle \int_S \boldsymbol{j} (\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = -\frac{\partial q}{\partial t}
$$これははじめに与えた表式であるので、これより示された。□
微分形の電荷の保存則
物理学の理論が進んでいくにつれ、遠く離れた場所が直接作用しあうのではなく、隣へ隣へと作用が通じて伝わっていくという見方が、より正確な理解を助けることがわかってきました。このすぐ隣同士の局所的な因果関係を記述するものは、積分形に対して微分形と呼ばれることが多いです。
いま紹介した電荷の保存則の記述は、ある空間領域全体での電荷の総和が保存されることを主張したもので、これに対して局所的な位置で電荷の総和が保存されることを主張した記述は、微分形の電荷の保存則といいます。
法則1.2(微分形の電荷の保存則)
以下のように記述する。ただし、\(\boldsymbol{j}(\boldsymbol{r})\)は各位置\(\boldsymbol{r}\)での電流密度を、\(\rho(\boldsymbol{r})\)は各位置\(\boldsymbol{r}\)での電荷密度を表す。
$$
\nabla \cdot \boldsymbol{j}(\boldsymbol{r})=-\frac{\partial \rho(\boldsymbol{r})}{\partial t}
$$
証明 ある閉曲面\(S\)をとり、その閉曲面内の空間領域を\(V\)とする。このとき、積分形の電荷の保存則より、
$$
\displaystyle \int_S \boldsymbol{j} (\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = -\frac{\partial q}{\partial t}
$$が成り立つ。ここで、左辺はガウスの発散定理より、
$$
\displaystyle \int_S \boldsymbol{j} (\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r}) dS = \displaystyle \int_V \nabla \cdot \boldsymbol{j} (\boldsymbol{r}) dV
$$と変形でき、右辺はある空間領域内での電荷の総合計は、その空間領域内で電荷密度を体積分した表式で与えられることから、
$$
q= \displaystyle \int_V \rho(\boldsymbol{r}) dV
$$と変形できるので、積分形の電荷の保存則は、
$$
\displaystyle \int_V \nabla \cdot \boldsymbol{j} (\boldsymbol{r}) dV = \displaystyle \int_V \frac{\partial \rho(\boldsymbol{r})}{\partial t} dV
$$と書き換えられることがわかる。いま、空間領域\(V\)は任意にとれるので、この関係がつねに成り立つには、
$$
\nabla \cdot \boldsymbol{j}(\boldsymbol{r})=-\frac{\partial \rho(\boldsymbol{r})}{\partial t}
$$でなくてはならない。これははじめに与えた表式であるので、これより示された。□
以上、電荷の保存則の積分形および微分形の記述と、その証明になります。


コメント