ベクトルポテンシャル

こんにちは、turtleです。現在物理学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

親記事で数学的道具として導入したスカラーポテンシャル$\phi$やベクトルポテンシャル$\boldsymbol{A}$について、とくに本稿で扱うベクトルポテンシャル$\boldsymbol{A}$の物理的な意味付けは、さまざまありますが、古典電磁気学の範囲で意味付けできるものとしては、「閉回路$C$上の位置$\boldsymbol{r}$における単位電流、単位長さあたりのエネルギーとみなせるもの」というものです。本稿ではこれを見た後、ゲージ変換について触れます。

ベクトルポテンシャルの意味付け
ゲージ変換

ベクトルポテンシャルの意味付け

ベクトルポテンシャルは、回転をとると磁場になるものという理解でも十分ですが、物理的な意味付けも今後重要になってくるため、ここではその一つとして、「閉回路$C$上の位置$\boldsymbol{r}$における単位電流、単位長さあたりのエネルギーとみなせるもの」だという意味付けを与えます。
これを説明するために、まずはいくつか補題を示していきます。

補題２.５.４(電流素片にはたらく力)
電流素片$Id \boldsymbol{l}$にはたらく力$d\boldsymbol{f}$は、$d\boldsymbol{f} = I(d \boldsymbol{l} \times \boldsymbol{B})$とかける。

補題２.５.４の証明

磁場$\boldsymbol{B}$中を速度$\boldsymbol{v}$で運動する電荷$q$が、磁場から受ける受けるローレンツ力は、$q(\boldsymbol{v} \times \boldsymbol{B})$であった。
ここで、断面積$S$、長さ$|d\boldsymbol{l}|$の微小な導線部分を考える。単位体積あたりの電荷の数(キャリア密度)を$n$、キャリア１個あたりの電荷量を$q$、電荷の平均速度を$\boldsymbol{v}$とすると、この微小な導線部分に含まれている電荷の総数$N$は、$N = nS|d\boldsymbol{l}|$となるので、微小部分全体に働く力$d\boldsymbol{f}$は、
$$
d\boldsymbol{f} = Nq\boldsymbol{v} \times \boldsymbol{B}= nSq |d\boldsymbol{l}| (\boldsymbol{v} \times \boldsymbol{B})
$$電流の定義は、単位時間当たりに通過する電荷量であるので、$I = nSq |\boldsymbol{v}|$であることから、$\boldsymbol{v} = |\boldsymbol{v}| \frac{d\boldsymbol{l}}{|d\boldsymbol{l}|}$とともに、もとの式に代入すると、以下が得られる。
$$
d\boldsymbol{f} = I (d\boldsymbol{l} \times \boldsymbol{B})
$$□

補題２.５.５
電流素片$Id \boldsymbol{l}$を微小に$d \boldsymbol{r}$動かすとき、外部磁場が及ぼす力に釣り合わせる外力のする仕事$dW$は、以下のように書ける。
$$
dW= I \boldsymbol{B} \cdot (d \boldsymbol{r} \times d \boldsymbol{l})= I\boldsymbol{B} \cdot \boldsymbol{n} dS
$$ただし、電流素片が通過した領域の面積を$dS$、この領域に垂直な$d \boldsymbol{r} \times d \boldsymbol{l}$方向の単位ベクトルを$\mathbf{n}$としている。

補題２.５.５の証明

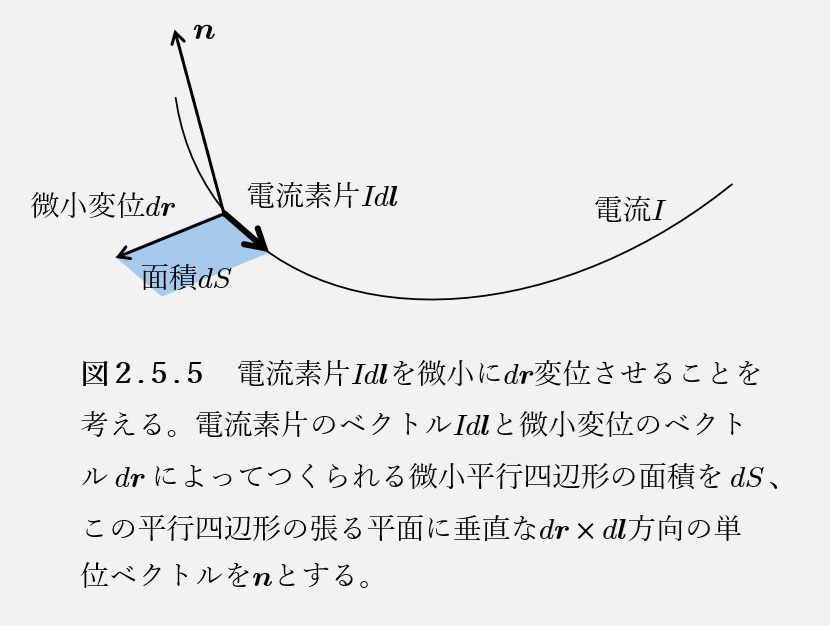
図２.５.５のように電流素片$Id \boldsymbol{l}$を微小に$d \boldsymbol{r}$動かすことを考える。
外部磁場が及ぼす力に釣り合わせる外力$d\boldsymbol{f}$は、補題２.５.４より、$d\boldsymbol{f}= -I(\boldsymbol{B} \times d \boldsymbol{l})$であるので、このとき外力のする仕事$dW$は、以下のように書ける。
$$
dW= \boldsymbol{f} \cdot d \boldsymbol{r} = -I(\boldsymbol{B} \times d \boldsymbol{l}) \cdot d \boldsymbol{r}
$$ここで、＞＞スカラー３重積より変形すると、$(\boldsymbol{B} \times d \boldsymbol{l}) \cdot d \boldsymbol{r} = \boldsymbol{B} \cdot (d \boldsymbol{r} \times d \boldsymbol{l})$になるので、$d \boldsymbol{r}$と$d \boldsymbol{l}$のつくる平行四辺形、つまり電流素片が通過した領域の面積$dS$、これに垂直な$d \boldsymbol{r} \times d \boldsymbol{l}$方向の単位ベクトル$\mathbf{n}$を用いて、次のように書ける。
$$
dW= I \boldsymbol{B} \cdot (d \boldsymbol{r} \times d \boldsymbol{l})= I\boldsymbol{B} \cdot \boldsymbol{n} dS
$$

補題２.５.６
静止した電流分布$\boldsymbol{j}(\boldsymbol{r})$が形成されているとき、その磁場中に存在する定常電流$I$の流れる閉回路$C_0$を変形したり移動したりして閉回路$C$とするときの、外部磁場が及ぼす力に釣り合わせる外力の仕事$W$は、
$$
W= -I \oint_C \boldsymbol{A} \cdot d \mathbf{r} + I \displaystyle \oint_{C_0} \boldsymbol{A} \cdot d \mathbf{r}
$$

補題２.５.６の証明

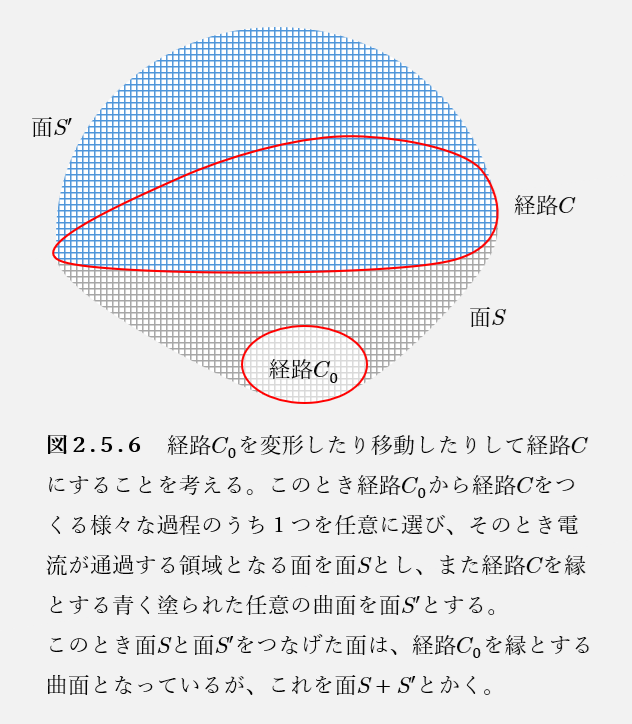
図２.５.６のように、面$S,S’,S+S’$を定義する。このとき、面$S$を通過して閉回路$C_0$を変形したり移動したりして閉回路$C$とするときの、外部磁場が及ぼす力に釣り合わせる外力のする仕事$W$を考える。これは、電流素片に対してする仕事を無数に足し合わせたものなので、補題２.５.５より、
$$
W= \displaystyle \int dW = I \displaystyle \int_S \boldsymbol{B} \cdot \boldsymbol{n} dS = I \displaystyle \int_S \left( \nabla \times \boldsymbol{A} \right) \cdot \boldsymbol{n} dS
$$とかくことができる。面積分の性質とストークスの定理から次の式が成り立つ。
$$
\int_{S’} \left( \nabla \times \boldsymbol{A} \right) \cdot \boldsymbol{n} dS = \int_{C} \boldsymbol{A} d\boldsymbol{r}
$$$$
\int_{S+S’} \left( \nabla \times \boldsymbol{A} \right) \cdot \boldsymbol{n} dS = \int_{C_0} \boldsymbol{A} d\boldsymbol{r}
$$$$
\int_{S} \left( \nabla \times \boldsymbol{A} \right) \cdot \boldsymbol{n} dS = \int_{S+S’} \left( \nabla \times \boldsymbol{A} \right) \cdot \boldsymbol{n} dS – \int_{S’} \left( \nabla \times \boldsymbol{A} \right) \cdot \boldsymbol{n} dS
$$以上３式を整理すると、これらより以下が成立する。
$$
W = \left( I \int_{C_0} \boldsymbol{A} d\boldsymbol{r} \right) – \left( I \int_{C} \boldsymbol{A} d\boldsymbol{r} \right)
$$□

ここで、注意をしておきますが、高校で扱ったであろう磁場によるローレンツ力は仕事をしないことと、電流を変位させるときに磁場が電流におよぼす力が仕事をすることは矛盾しません。
というのは、電流の流れる閉回路を変形したり移動したりするとき、電流を流れる電荷は、電流の方向(閉回路に沿った方向)と外力による変形や移動の方向の２方向に速度成分をもっています。ここでたしかに、各方向に対するローレンツ力成分の仕事の和は、電荷の移動方向と合成した力が直交するので０になりますが、各方向に対するローレンツ力成分の仕事それぞれは、電荷の移動方向とローレンツ力成分が直交していないため、有限の仕事をすることができるのです。

さて示す補題はここまでです。
補題２.５.６より、任意の閉回路$C$に対して、その分布状態を基準の閉回路$C_0$から作るときの電気的な力に釣り合わせる外力の仕事$W_{C_0 \rightarrow C}$が、作る過程によらず等しくなります。このとき、基準状態$C_0$から閉回路を動かさない、あるいは一度動かしてもう一度元の閉回路$C_0$に戻すときの仕事はつねに０であるので、回路の形を$C_0$から$C$、そしてまた$C_0$へ戻すことを考えると、
$$
W_{C_0 \rightarrow C}+W_{C \rightarrow C_0}=0
$$となります。これを移項すると、$W_{C \rightarrow C_0}=-W_{C_0 \rightarrow C}$となるので、磁場が電流におよぼす力自身のする仕事とそれに釣り合わせる外力のする仕事は逆符号であることから、この閉回路$C$が基準の閉回路$C_0$に戻るときには、磁場が電流におよぼす力が一定値$W_{C_0 \rightarrow C}$だけの仕事をすることがわかりますね。

これはつまり、物理的な表現をすると、ある閉回路に対してエネルギーを定義できるということです。数式を使って書くと、磁場中に存在する定常電流$I$の流れる閉回路$C$は、位置エネルギーのようなもの$U(C)$をもっていると考えることができ、それは
$$
U(C)-U(C_0)=-I \displaystyle \oint_C \boldsymbol{A} \cdot d \boldsymbol{r} + I \displaystyle \oint_{C_0} \boldsymbol{A} \cdot d \boldsymbol{r}
$$を満足するということでした。ここで、基準の$C_0$として一点に収束した閉回路をとることを考えます。一点に収束した閉回路のエネルギーは０であるので、改めてその閉回路がない状態を基準とした、定常電流$I$の流れる閉回路$C$のもつエネルギーを$U(C)$と定義すると、
$$
U(C)=-I \displaystyle \oint_C \boldsymbol{A} \cdot d \boldsymbol{r}
$$となりますね。この式を見ると、積分の中身$-\boldsymbol{A}(\boldsymbol{r})$は閉回路$C$上の位置$\boldsymbol{r}$における単位電流、単位長さあたりのエネルギーとしてみなすことができることが分かるかと思います(これ自体はベクトルですが、表式としてそういう役割をしているということです)。
本稿では、これを古典電磁気学の範囲におけるベクトルポテンシャルの意味付けとしました。

ゲージ変換

さて話を変えて、親記事においては、以下のような流れでスカラーポテンシャル$\phi$やベクトルポテンシャル$\boldsymbol{A}$を導入したのでした。

定理２.５
電場$\boldsymbol{E}$、磁場$\boldsymbol{B}$について、
$$
\boldsymbol{E} = -\nabla \phi – \frac{\partial \boldsymbol{A}}{\partial t}
$$$$
\boldsymbol{B} = \nabla \times \boldsymbol{A}
$$なるスカラー場$\phi$とベクトル場$\boldsymbol{A}$が必ず存在する。

定義２.６(スカラーポテンシャル、ベクトルポテンシャルの定義
定理２.５におけるスカラー場$\phi$とベクトル場$\boldsymbol{A}$を、それぞれスカラーポテンシャル、ベクトルポテンシャルと定義する。

つまり、定理２.５であげられているこの２式
$$
\boldsymbol{E} = -\nabla \phi – \frac{\partial \boldsymbol{A}}{\partial t}
$$$$
\boldsymbol{B} = \nabla \times \boldsymbol{A}
$$を満たすスカラー場$\phi$とベクトル場$\boldsymbol{A}$ならば、どんなものでも、スカラーポテンシャル$\phi$やベクトルポテンシャル$\boldsymbol{A}$の定義を満たしているということです。このことから、スカラーポテンシャル$\phi$やベクトルポテンシャル$\boldsymbol{A}$にはいくらかの自由度があることがわかります(一意に定まらなくてもおかしくありません)。
実際に、次のことがわかっています。

定理２.５.７(ゲージ変換)
あるスカラー場$\phi$とベクトル場$\boldsymbol{A}$が、$\boldsymbol{E} = -\nabla \phi – \frac{\partial \boldsymbol{A}}{\partial t}$と$\boldsymbol{B} = \nabla \times \boldsymbol{A}$を満たすとき、適当なスカラー関数$\chi(\boldsymbol{r}, t)$に対して、
$$
\phi’ = \phi – \frac{\partial \chi}{\partial t} \quad \quad \boldsymbol{A}’ = \boldsymbol{A} + \nabla \chi
$$とすると、このスカラー場$\phi’$とベクトル場$\boldsymbol{A}’$も、$\boldsymbol{E} = -\nabla \phi’ – \frac{\partial \boldsymbol{A}’}{\partial t}$と$\boldsymbol{B} = \nabla \times \boldsymbol{A}’$を満足する。

定理２.５.７の証明

第１式、第２式についてそれぞれ以下が成り立つ。
$$
-\nabla \phi’ – \frac{\partial \boldsymbol{A}’}{\partial t} = -\nabla \left( \phi – \frac{\partial \chi}{\partial t} \right) – \frac{\partial}{\partial t} (\boldsymbol{A} + \nabla \chi) = -\nabla \phi + \nabla \left( \frac{\partial \chi}{\partial t} \right) – \frac{\partial \boldsymbol{A}}{\partial t} – \frac{\partial (\nabla \chi)}{\partial t} = -\nabla \phi – \frac{\partial \boldsymbol{A}}{\partial t} = \boldsymbol{E}
$$$$
\nabla \times \boldsymbol{A}’ = \nabla \times (\boldsymbol{A} + \nabla \chi) = \nabla \times \boldsymbol{A} + \nabla \times (\nabla \chi) = \nabla \times \boldsymbol{A} = \boldsymbol{B}
$$よって、示された。□

この$\chi(\boldsymbol{r}, t)$を用意して、$\boldsymbol{A}$と$\phi$を書き換えることをゲージ変換とよんでいます。物理的には$\phi$と$\boldsymbol{A}$は数学の道具にすぎず、$\boldsymbol{E}$と$\boldsymbol{B}$が求められればなんでもよいともいえるので、それならばそれぞれの問題や場合によって一番計算しやすい形に$\phi$と$\boldsymbol{A}$を変換しよう、というのがゲージ変換のモチベーションです。
とくに、代表的なゲージとして次の２つがあります。

(1)クーロンゲージ条件$\nabla \cdot \boldsymbol{A} = 0$
静電気の問題や、原子レベルの計算で便利なゲージ条件で、$\phi$の計算が簡単になります。

(2)ローレンツゲージ条件 $\nabla \cdot \boldsymbol{A} + \epsilon_0 \mu_0 \frac{\partial \phi}{\partial t} = 0$
電磁波や相対性理論の問題でとても便利なゲージ条件で、$\phi$と$\boldsymbol{A}$が対等な形になって波の方程式がきれいに導けます。

では最後に、クーロンゲージ条件をみたすベクトルポテンシャル$\boldsymbol{A}$の取り方を紹介しましょう。

定理２.５.８
ある位置$\boldsymbol{r’}$における電流密度を$j(\boldsymbol{r’})$とすると、位置$\boldsymbol{r}$におけるベクトルポテンシャル$\boldsymbol{A}(\boldsymbol{r})$の取り方の１つは、
$$
\boldsymbol{A}(\boldsymbol{r})=\frac{\mu_0}{4 \pi} \displaystyle \int_{V’} \frac{\boldsymbol{j}(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|} dV’
$$であって、これはクーロンゲージ条件$\nabla \cdot \boldsymbol{A} = 0$を満たす。

定理２.５.８の証明

はじめに、与えられた表式がベクトルポテンシャル$\boldsymbol{A}(\boldsymbol{r})$として正しいことを示す。
$$
\boldsymbol{A}(\boldsymbol{r})=\frac{\mu_0}{4 \pi} \displaystyle \int_{V’} \frac{\boldsymbol{j}(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|} dV’
$$の回転をとる。$\nabla$は位置$\boldsymbol{r}$における微分演算子なので、位置$\boldsymbol{r’}$の関数はすべて定数として扱え、$\nabla$は積分の中に入れることができるから、
$$
\nabla \times \displaystyle \int_{V’} \frac{\mu_0}{4 \pi} \frac{\boldsymbol{j}(\mathbf{r’})}{|\mathbf{r}-\mathbf{r’}|} dV’ = \frac{\mu_0}{4 \pi} \displaystyle \int_{V’} \left( \nabla \times \frac{\boldsymbol{j}(\mathbf{r’})} {|\mathbf{r}-\mathbf{r’}|} \right) dV’
$$とかける。被積分関数を取り出してその$x$成分を計算すると、
$$
\left[ \nabla \times \frac{\boldsymbol{j}(\boldsymbol{r’})} {|\boldsymbol{r}-\boldsymbol{r’}|} \right]_x = \frac{\partial}{\partial y} \frac{j_z(\boldsymbol{r’})}{\sqrt{(x-x’)^2+(y-y’)^2+(z-z’)^2}}-\frac{\partial}{\partial z} \frac{j_y(\boldsymbol{r’})}{\sqrt{(x-x’)^2+(y-y’)^2+(z-z’)^2}}
$$位置$\boldsymbol{r’}$の関数はすべて定数として扱えるので、微分の外に出すことができる。
$$
\frac{\partial}{\partial y} \frac{i_z(\boldsymbol{r’})}{\sqrt{(x-x’)^2+(y-y’)^2+(z-z’)^2}}= j_z(\boldsymbol{r’}) \frac{y-y’}{\sqrt{(x-x’)^2+(y-y’)^2+(z-z’)^2}^3}
$$$$
\frac{\partial}{\partial z} \frac{i_y(\boldsymbol{r’})}{\sqrt{(x-x’)^2+(y-y’)^2+(z-z’)^2}} = j_y(\boldsymbol{r’}) \frac{z-z’}{\sqrt{(x-x’)^2+(y-y’)^2+(z-z’)^2}^3}
$$であることから、もとの式に代入すると、
$$
\left[ \nabla \times \frac{\boldsymbol{j}(\boldsymbol{r’})} {|\boldsymbol{r}-\boldsymbol{r’}|} \right]_x = \left[ \frac{\boldsymbol{j}(\mathbf{r’}) \times (\mathbf{r}-\mathbf{r’})}{|\mathbf{r}-\mathbf{r’}|^3} \right]_x
$$であるので、各成分の対称性より、以下が示される。
$$
\nabla \times \displaystyle \int_{V’} \frac{\mu_0}{4 \pi} \frac{\boldsymbol{j}(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|} dV’ = \displaystyle \int_{V’} \frac{\mu_0}{4 \pi} \frac{\boldsymbol{j}(\boldsymbol{r’}) \times (\boldsymbol{r}-\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|^3} dV’ = \boldsymbol{B}(\boldsymbol{r})
$$
続いて、与えられた表式がクーロンゲージ条件を満たすこと、つまり、
$$
\boldsymbol{A}(\boldsymbol{r})=\frac{\mu_0}{4 \pi} \displaystyle \int_{V’} \frac{\boldsymbol{j}(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|} dV’
$$の発散が０になることをいう。$A_x$の$x$方向における偏微分は、
$$
\frac{\partial A_x}{\partial x} = \frac{\mu_0}{4 \pi} \displaystyle \int_{V’} i_x(\boldsymbol{r’}) \frac{\partial}{\partial x} \left( \frac{1}{|\boldsymbol{r}-\boldsymbol{r’}|} \right) dV’
$$とかける。ここで、微分に関して以下の２つの式を用いる。第１式は$|\boldsymbol{r}-\boldsymbol{r’}|=\sqrt{(x-x’)^2+(y-y’)^2+(z-z’)^2}$として両辺微分してみると直ちに導かれる式で、第２式は積の微分法則の順番を入れ替えたものである。
$$
\frac{\partial}{\partial x} \left( \frac{1}{|\boldsymbol{r}-\boldsymbol{r’}|} \right)= – \frac{\partial}{\partial x’} \left( \frac{1}{|\boldsymbol{r}-\boldsymbol{r’}|} \right)
$$$$
j_x(\boldsymbol{r’}) \frac{\partial}{\partial x’} \left( \frac{1}{|\boldsymbol{r}-\boldsymbol{r’}|} \right) = \frac{\partial}{\partial x’} \left( \frac{j_x(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|}\right) – \frac{\partial j_x(\boldsymbol{r’})}{\partial x’} \frac{1}{|\boldsymbol{r}-\boldsymbol{r’}|}
$$これを用いると、$A_x$の$x$方向における偏微分は、以下のようになる。
$$
\frac{\mu_0}{4 \pi} \displaystyle \int_{V’} j_x(\boldsymbol{r’}) \frac{\partial}{\partial x} \left( \frac{1}{|\boldsymbol{r}-\boldsymbol{r’}|} \right) dV’ = \frac{\mu_0}{4 \pi} \displaystyle \int_{V’} \frac{\partial j_x(\boldsymbol{r’})}{\partial x’} \frac{1}{|\boldsymbol{r}-\boldsymbol{r’}|} dV’ – \frac{\mu_0}{4 \pi} \displaystyle \int_{V’} \frac{\partial}{\partial x’} \left( \frac{j_x(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|}\right) dV’
$$$A_y$の$y$方向、$A_z$の$z$方向における偏微分も、対称性より同じように変形できるので、以下のようになる。ただし$\nabla ‘$は、位置$\boldsymbol{r’}$における微分演算子という意味である。
$$
\nabla \cdot \boldsymbol{A}= \frac{\mu_0}{4\pi} \displaystyle \int_{V’} \frac{\nabla ‘ \boldsymbol{j}(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|} dV’ – \frac{\mu_0}{4 \pi} \displaystyle \int_{V’} \nabla ‘ \cdot \left( \frac{\boldsymbol{j}(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|}\right) dV’
$$第１項については、定常電流は$\nabla ‘ \boldsymbol{j}(\boldsymbol{r’})=0$を満たすことから０となる。第２項については、ガウスの発散定理を用いることで、
$$
\frac{\mu_0}{4 \pi} \displaystyle \int_{V’} \nabla ‘ \cdot \left( \frac{\boldsymbol{j}(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|} \right) dV’ = \displaystyle \int_{S’} \left( \frac{\boldsymbol{j}(\boldsymbol{r’})}{|\boldsymbol{r}-\boldsymbol{r’}|} \right) \cdot \boldsymbol{n} dS’
$$のように、全空間の表面における面積分と変形できる。電流の分布は有限の範囲に限られているので、全空間の表面では電流密度が０になることから、体積分は０になる。
以上より、$\nabla \cdot \boldsymbol{A}=0$であることが示された。□