こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。
本稿では、導体のある空間における電磁気現象の例として、電気容量やコンデンサーをみていきます。
孤立導体の電気容量
半径\(R\)の導体球に電荷\(q\)を与えたとき、導体外部の真空領域における静電場は
$$
\boldsymbol{E}(\boldsymbol{r})=\frac{q}{4\pi\epsilon_0}\frac{\boldsymbol{r}}{r^2}\quad(r>R)
$$であり、ここから無限遠を基準とした半径\(R\)の導体球の電位\(\phi\)を求めると、無限遠から導体球表面までの任意の経路を\(C\)としたとき、
$$
\phi=\displaystyle \int_{C} \boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r} = \frac{q}{4\pi \epsilon_0 R}
$$となります。ここで、\(\frac{1}{4\pi \epsilon_0 R}\)はこの空間あるいは導体球に特有の定数であるため、導体球の蓄える電荷\(q\)と導体球の電位\(\phi\)は比例することが分かります。これは導体球に限った話ではなく、一般に以下が成り立ちます。
定理5.1(孤立導体の電気容量)
無限に広い自由空間中に電荷\(q\)を帯びた導体のみが置かれているとき、この導体の構造や形状が同じならば、蓄える電荷\(q\)と電位\(\phi\)は比例関係\(q=C\phi\)にある。この比例定数\(C\)を一般に電気容量とよぶ。
証明 無限に広い自由空間中に電荷\(q\)を帯びた導体のみが置かれていることを考える。このときの金属表面\(S\)上の位置\(\boldsymbol{r}\)における電荷面密度を\(\sigma(\boldsymbol{r})\)とすると、無限遠を基準とした金属表面上の位置\(\boldsymbol{r}_0\)における電位\(\phi\)は、
$$
\phi=\displaystyle \int_{V’} \frac{\rho(\boldsymbol{r’})dV’}{4\pi\epsilon_0|\boldsymbol{r}-\boldsymbol{r’}|}=\frac{1}{4\pi\epsilon_0} \displaystyle \int_{S} \frac{\sigma(\boldsymbol{r})}{|\boldsymbol{r}-\boldsymbol{r}_0|} dS
$$ここで金属表面における電荷分布は、金属内部で電場が打ち消されるように自由電子が動いた結果であるから、金属の構造や形状が同じならば、帯びている電荷の量にのみ比例する。つまり、任意に選んだある位置\(\boldsymbol{r}\)において、\(\sigma(\boldsymbol{r}) \propto q\)であるので、
$$
\frac{1}{4\pi\epsilon_0} \displaystyle \int_{S} \frac{\sigma(\boldsymbol{r})}{|\boldsymbol{r}-\boldsymbol{r}_0|} dS \propto q \left( \displaystyle \int_{S} \frac{dS}{4\pi\epsilon_0|\boldsymbol{r}-\boldsymbol{r}_0|} \right)
$$\(\displaystyle \int_{S} \frac{dS}{4\pi\epsilon_0|\boldsymbol{r}-\boldsymbol{r}_0|}\)は、金属の構造や形状が定まっているとき一定の値をとるので、示された。□
複数の導体系の電気容量
この段落では、別記事で示した定理を、以下のように番号を振って証明なしで用います。
定理1(系5.7)
電荷分布\(\rho_1(\boldsymbol{r})\)と境界条件\(C_1\)に対するポアソンの方程式の解を\(\phi_1(\boldsymbol{r})\)、電荷分布\(\rho_2(\boldsymbol{r})\)と境界条件\(C_2\)に対するポアソンの方程式の解を\(\phi_2(\boldsymbol{r})\)とすると、電荷分布\(\rho_1(\boldsymbol{r})+\rho_2(\boldsymbol{r})\)と境界条件\(C_1+C_2\)に対するポアソンの方程式の解は\(\phi(\boldsymbol{r})=\phi_1(\boldsymbol{r})+\phi_2(\boldsymbol{r})\)である。
ただし、条件\(C_1+C_2\)とは、たとえば、条件\(C_1\)が”各点で\(\phi_1(\boldsymbol{r})\)が連続で位置\(r_0\)において\(\phi_1(\boldsymbol{r}_0)=a_1\)”、条件\(C_2\)が”各点で\(\phi_2(\boldsymbol{r})\)が連続で位置\(r_0\)において\(\phi_2(\boldsymbol{r}_0)=a_2\)”であるときならば、条件\(C_1+C_2\)は”各点で\(\phi(\boldsymbol{r})\)が連続で位置\(r_0\)において\(\phi(\boldsymbol{r}_0)=a_1+a_2\)である”といったように、各条件の和に対応する条件とする。
定理2
導体表面における電荷面密度を\(\sigma(\boldsymbol{r})\)、導体表面における電場を\(\boldsymbol{E}(\boldsymbol{r})\)としたとき、\(\sigma(\boldsymbol{r})=\epsilon_0 E(\boldsymbol{r})\)
定理3(系5.5の証明の一部)
各位置\(\boldsymbol{r}\)での電位を\(\phi(\boldsymbol{r})\)としたとき、電位の方向微分について以下が成立する。
$$
\frac{\partial \phi}{\partial \boldsymbol{n}} = \nabla \phi(\boldsymbol{r}) \cdot \boldsymbol{n}
$$
これをふまえて、この段落で証明する複数の導体系について成り立つ定理は、以下です。
定理5.2(複数の導体系の電気容量)
無限に広い自由空間中に電荷\(Q_1\),\(Q_2\)を帯びた2つの導体1と2が置かれているとき、これらの導体の構造や形状、位置関係が同じならば、1と2に蓄えられる電荷はいずれも、導体1の電位\(\phi_1\)に比例する項と、導体2の電位\(\phi_2\)に比例する項の足し合わせになる。
$$
Q_1=C_{11} \phi_1+C_{12} \phi_2
$$$$
Q_2=C_{21} \phi_1+C_{22} \phi_2
$$とかいたときの\(C_{11}\),\(C_{21}\),\(C_{12}\),\(C_{22}\)を電気容量係数という。
証明 定理1より、導体1の電位が\(\phi_1\)、導体2の電位が\(\phi_2\)であるときの導体外部の領域での無限遠を基準とした電位\(\phi(\boldsymbol{r})\)は、導体1の電位が\(\phi_1\)、導体2の電位が\(0\)のときの導体外部の領域での無限遠を基準とした電位\(\phi_1(\boldsymbol{r})\)と、導体1の電位が\(0\)、導体2の電位が\(\phi_2\)のときの導体外部の領域での無限遠を基準とした電位\(\phi_2(\boldsymbol{r})\)の和となる。
導体1の電位が\(\phi_1\)、導体2の電位が\(0\)のときの、導体1と2の表面\(S_1\),\(S_2\)上の位置\(\boldsymbol{r}\)における電荷面密度をそれぞれ\(\sigma_{11}(\boldsymbol{r})\),\(\sigma_{21}(\boldsymbol{r})\)として、導体1の電位が\(0\)、導体2の電位が\(\phi_2\)のときの、金属1と2の表面\(S_1\),\(S_2\)上の位置\(\boldsymbol{r}\)における電荷面密度をそれぞれ\(\sigma_{12}(\boldsymbol{r})\),\(\sigma_{22}(\boldsymbol{r})\)とする。
このとき、導体1の表面\(S_1\)上の位置\(\boldsymbol{r}\)において、定理2と3より、
$$
-\frac{\partial \phi_1(\boldsymbol{r})}{\partial \boldsymbol{n}}=\frac{\sigma_{11}(\boldsymbol{r})}{\epsilon_0}
$$$$
-\frac{\partial \phi_1(\boldsymbol{r})}{\partial \boldsymbol{n}}=\frac{\sigma_{21}(\boldsymbol{r})}{\epsilon_0}
$$が成り立つ。同様に、導体2の表面\(S_2\)上の位置\(\boldsymbol{r}\)において、定理2と3より、
$$
-\frac{\partial \phi_2(\boldsymbol{r})}{\partial \boldsymbol{n}}=\frac{\sigma_{12}(\boldsymbol{r})}{\epsilon_0}
$$$$
-\frac{\partial \phi_2(\boldsymbol{r})}{\partial \boldsymbol{n}}=\frac{\sigma_{22}(\boldsymbol{r})}{\epsilon_0}
$$が成り立つ。以上4式より、導体の構造や形状、位置関係が同じとき、\(\sigma_{11}(\boldsymbol{r})\),\(\sigma_{21}(\boldsymbol{r})\)はいずれも\(\phi_1\)と、\(\sigma_{12}(\boldsymbol{r})\),\(\sigma_{22}(\boldsymbol{r})\)はいずれも\(\phi_2\)と比例関係にある…(*)。
導体1の電位が\(\phi_1\)、導体2の電位が\(\phi_2\)であるときに、導体外部の領域での空間における無限遠を基準とした電位\(\phi(\boldsymbol{r})\)は、\(\phi_1(\boldsymbol{r})+\phi_2(\boldsymbol{r})\)であるから、
$$
Q_1=-\epsilon_0 \displaystyle \int_{S_1} \frac{\partial \{ \phi_1(\boldsymbol{r})+\phi_2(\boldsymbol{r}) \} }{\partial \boldsymbol{n}}=\displaystyle \int_{S_1} [\sigma_{11}(\boldsymbol{r})+\sigma_{12}(\boldsymbol{r})] dS
$$$$
Q_2=-\epsilon_0 \displaystyle \int_{S_2} \frac{\partial \{ \phi_1(\boldsymbol{r})+\phi_2(\boldsymbol{r}) \} }{\partial \boldsymbol{n}}=\displaystyle \int_{S_2} [\sigma_{21}(\boldsymbol{r})+\sigma_{22}(\boldsymbol{r})] dS
$$であるので、(*)より示される。□
なお、導体の数が3個以上でも同じような関係が一般に成立する。
相反定理
定理5.3(電気容量係数の相反定理)
導体の構造や形状、位置関係が同じとき、1と2に蓄えられる電荷をそれぞれ、
$$
Q_1=C_{11} \phi_1+C_{12} \phi_2
$$$$
Q_2=C_{21} \phi_1+C_{22} \phi_2
$$とかいたときの電気容量係数\(C_{11}\),\(C_{21}\),\(C_{12}\),\(C_{22}\)について、必ず\(C_{12}=C_{21}\)が成立する。
証明 無限に広い自由空間中に電荷\(Q_1\),\(Q_2\)を帯びた2つの導体1と2が置かれているとき、電荷\(Q_1\),\(Q_2\)を帯びた電位\(\phi_1\),\(\phi_2\)の導体の静電エネルギー\(U\)は、
$$
U=\frac{1}{2} \displaystyle \int_{V} \rho(\boldsymbol{r})\phi(\boldsymbol{r})dV =\frac{1}{2} Q_1 \phi_1 +\frac{1}{2} Q_2 \phi_2
$$電気容量係数の定義より、
$$
Q_1=C_{11} \phi_1+C_{12} \phi_2
$$$$
Q_2=C_{21} \phi_1+C_{22} \phi_2
$$であるので、ここから\(\phi_1\),\(\phi_2\)について逆に解くと、
$$
\phi_1=\frac{C_{22}Q_1-C_{12}Q_2}{C_{11}C_{22}-C_{12}C_{21}}
$$$$
\phi_2=\frac{C_{11}Q_2-C_{21}Q_1}{C_{11}C_{22}-C_{12}C_{21}}
$$これを静電エネルギーの表式に代入すると、
$$
U=\frac{1}{2}\frac{C_{22}Q_1^2-(C_{12}+C_{21})Q_1Q_2+C_{11}Q_2^2}{C_{11}C_{22}-C_{12}C_{21}}
$$とかける。ここで、導体1の電荷を\(Q_1\)から\(Q_1+\Delta Q_1\)にしたときの、静電エネルギーの変化\(\Delta U\)を、微小項\(\Delta Q_1\)の1次の項まで求めることを考える。エネルギーの変化から求めると、
$$
\Delta U=[\frac{1}{2}\frac{C_{22}(Q_1+\Delta Q_1)^2-(C_{12}+C_{21})(Q_1+\Delta Q_1)Q_2+C_{11}Q_2^2}{C_{11}C_{22}-C_{12}C_{21}}]-[\frac{1}{2}\frac{C_{22}Q_1^2-(C_{12}+C_{21})Q_1Q_2+C_{11}Q_2^2}{C_{11}C_{22}-C_{12}C_{21}}] \simeq \frac{1}{2}\frac{2C_{22}Q_1-(C_{12}+C_{21})Q_2}{C_{11}C_{22}-C_{12}C_{21}} \Delta Q_1
$$一方で導体1の電荷を\(Q_1\)から\(Q_1+\Delta Q_1\)にするために、無限遠から微小電荷\(\Delta Q_1\)を運んだときの、静電気力に釣り合わせた外力の仕事として考えると、
$$
\Delta U \simeq \phi_1 \Delta Q_1=\frac{C_{22}Q_1-C_{12}Q_2}{C_{11}C_{22}-C_{12}C_{21}} \Delta Q_1
$$ゆえに、2つの表式を比較すると、エネルギー変化の量は等しいことから
$$
C_{12}+C_{21}=2C_{12}
$$が要請され、これより示された。□
コンデンサー
ここまで示したように、導体の構造や形状、位置関係が同じとき、1と2に蓄えられる電荷はいずれも、導体1の電位\(\phi_1\)に比例する項と、導体2の電位\(\phi_2\)に比例する項の足し合わせになるのでした。つまり逆に解くと、1と2の電位\(\phi_1\),\(\phi_2\)はいずれも、導体1に蓄えられる電荷\(Q_1\)に比例する項と、導体2に蓄えられる電荷\(Q_2\)に比例する項の足し合わせになるということです。
ここで2つの導体に、同じ大きさで逆符号の電荷\(\pm Q\)を与えることを考えましょう。このとき1と2の電位\(\phi_1\),\(\phi_2\)はいずれも、\(+Q\)に比例する項と\(-Q\)に比例する項の足し合わせになるので、\(Q\)に比例します。
ゆえに、2つの電位差\(\Delta \phi =\phi_1-\phi_2\)も\(Q\)に比例することになりますから、有名な結論として以下が成り立ちます。
定義5.4(コンデンサーの定義)
2つの導体に同じ大きさで逆符号の電荷\(\pm Q\)を与えることで、互いのポテンシャルを高めずに多量の電荷を蓄える装置をコンデンサーという。コンデンサーを構成する2つの導体の構造や形状、位置関係が同じとき、蓄える電荷\(q\)と電位差\(\Delta \phi\)は比例関係\(q=C\Delta \phi\)にある。この比例定数\(C\)を一般に電気容量とよぶ。
有名なコンデンサーとして平板コンデンサーと同心球形コンデンサーについて、その表面電荷分布やその導体の間に生じる電場、電位差、電気容量、静電エネルギーを紹介します。つねに表面電荷分布→電場→電位差→電気容量→静電エネルギーの順で考えていくと迷いにくいです。
平板コンデンサー
例5.5(平板コンデンサー)
断面積\(S\)で距離が\(d\)である無限に広い平板コンデンサーに同じ大きさで逆符号の電荷\(\pm Q\)を与えると、導体板の互いに向かい合う面に一様面密度\(\frac{\pm Q}{S}\)の表面電荷分布、\(+Q\)の極板から\(-Q\)の極板へ\(E=\frac{Q}{\epsilon_0 S}\)の一様静電場、\(\Delta \phi=\frac{Qd}{\epsilon_0 S}\)の電位差が生じることを順に導くことができる。
これより、この平板コンデンサーの電気容量は\(C=\frac{Q}{\Delta \phi}=\frac{\epsilon_0 S}{d}\)であり、静電エネルギーは
$$
U=\frac{Q\Delta \phi}{2}=\frac{C (\Delta \phi)^2}{2}=\frac{Q^2}{2C}=\frac{Q^2 d}{2\epsilon_0 S}=\frac{\epsilon_0 E^2}{2} Sd
$$のような表式で与えられる。
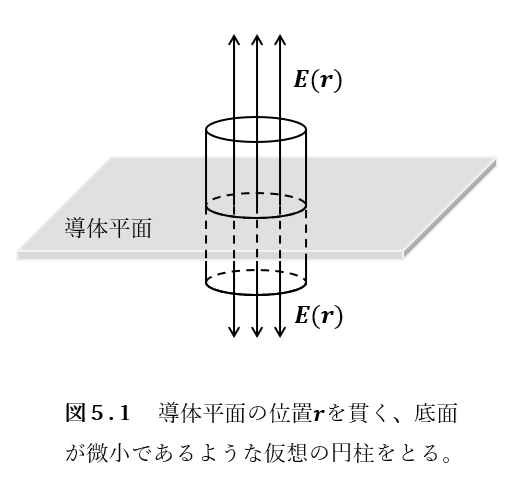
証明 一様電荷面密度\(\sigma\)の無限に広い電荷分布が単独で存在するとき、つくられる電場を考える。無限に広いという仮定は、端のことを無視して一様電荷分布上のどこも区別できないとしてよいという意味を含んでいるので、電場もいたるところ一様であることより、空間の対称性から電場は電荷の分布する平面に垂直であることが要請される。
図5.1のように、電荷の分布する平面を貫く仮想の円柱に対して積分形のガウスの法則を適用すると、
$$
E=\frac{\sigma}{2\epsilon_0}
$$
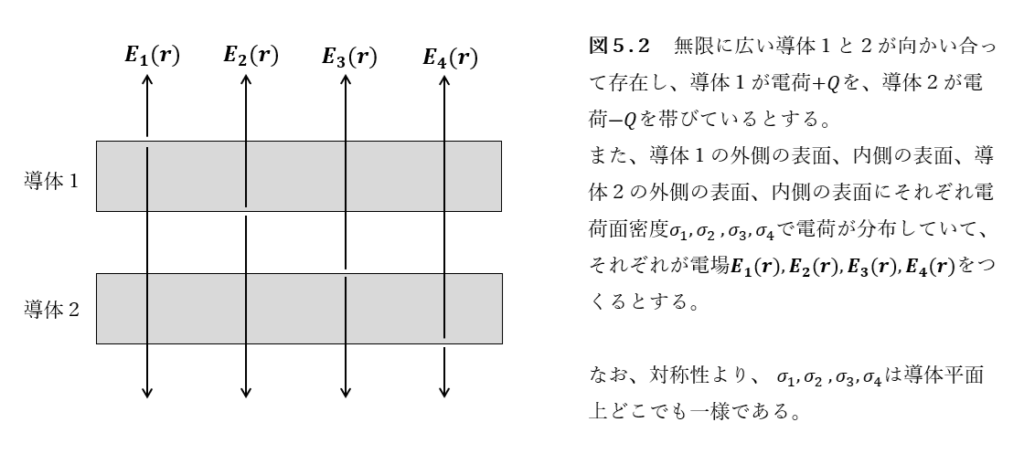
ここで、無限に広い平板コンデンサーという仮定も、端のことを無視してコンデンサーの極板間のどこも区別できず一様であるとしてよいという意味を含んでいるので、\(\sigma_1\),\(\sigma_2\),\(\sigma_3\),\(\sigma_4\)は場所によらず一定である。
図2のように、\(\sigma_1\),\(\sigma_2\),\(\sigma_3\),\(\sigma_4\)がそれぞれ単独で作る電場を\(\boldsymbol{E}_1\),\(\boldsymbol{E}_2\),\(\boldsymbol{E}_3\),\(\boldsymbol{E}_4\)とすると、これらの大きさは\(i=1,2,3,4\)に対してそれぞれ\(E_i=\frac{\sigma_i}{2\epsilon_0}\)を満たしている。
物理的な要請として、電荷保存則から、
$$
\sigma_1 S+\sigma_2 S=Q
$$$$
\sigma_3 S+\sigma_4 S=-Q
$$金属内部の電場は\(\boldsymbol{0}\)であることから、
$$
E_1-E_2-E_3-E_4=\frac{\sigma_1-\sigma_2-\sigma_3-\sigma_4}{2\epsilon_0}=0
$$$$
E_1+E_2+E_3-E_4=\frac{\sigma_1+\sigma_2+\sigma_3-\sigma_4}{2\epsilon_0}=0
$$以上4式より、\(\sigma_1\),\(\sigma_2\),\(\sigma_3\),\(\sigma_4\)を解くと、
$$
\sigma_1=\sigma_4=0 \qquad \sigma_2=\frac{Q}{S} \qquad \sigma_3=-\frac{Q}{S}
$$として、導体板の互いに向かい合う面に一様面密度\(\frac{\pm Q}{S}\)の表面電荷分布が生じていることが導かれる。
これより、電場は、\(+Q\)の極板から\(-Q\)の極板へ
$$
E=E_1+E_2-E_3-E_4=\frac{\sigma_1+\sigma_2-\sigma_3-\sigma_4}{2\epsilon_0}=\frac{Q}{\epsilon_0 S}
$$として一様に形成される。電位差は、\(-Q\)の極板から\(+Q\)の極板へ単位電荷を運ぶときに、静電気力に釣り合わせる外力の仕事を考えると、
$$
\Delta \phi=Ed=\frac{Qd}{\epsilon_0 S}
$$となる。平板コンデンサーの電気容量や静電エネルギーは、いま求めた表式と定義に沿って計算すると直ちに示される。□
同心球形コンデンサー
続いて図5.3のように、内側の導体球が\(+Q\)、外側の導体球殻が\(-Q\)を帯びているような、同心球形コンデンサーについて考えます。
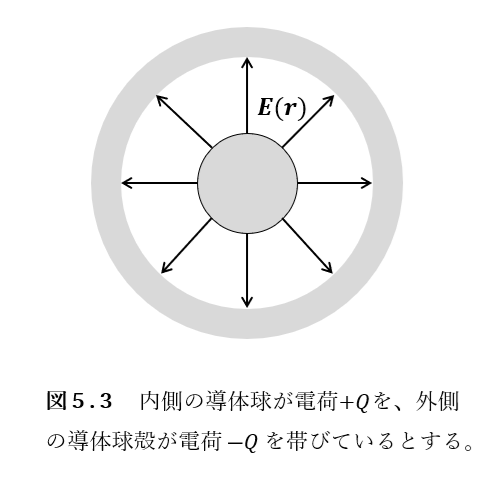
例5.6(同心球形コンデンサー)
内側の導体球の半径が\(a\)、外側の導体球殻の半径が\(b\)である同心球形コンデンサーに同じ大きさで逆符号の電荷\(\pm Q\)を与えると、内側の導体表面に一様面密度\(\frac{Q}{4\pi a^2}\)、導体球殻の導体球と向かい合う側に一様面密度\(-\frac{Q}{4\pi b^2}\)の球対称電荷分布、導体球の中心を原点として極板間のみに\(\boldsymbol{E}(\boldsymbol{r})=\frac{Q}{4\pi \epsilon_0}\frac{\boldsymbol{r}}{r^3}\)の静電場、\(\Delta \phi=\frac{Q}{4\pi \epsilon_0}(\frac{1}{a}-\frac{1}{b})\)の電位差が生じることを順に導くことができる。
これより、この平板コンデンサーの電気容量は\(C=\frac{Q}{\Delta \phi}=\frac{4\pi\epsilon_0 ab}{b-a}\)であり、静電エネルギーは
$$
U=\frac{Q\Delta \phi}{2}=\frac{C (\Delta \phi)^2}{2}=\frac{Q^2}{2C}=\frac{Q^2 (b-a)}{8\pi \epsilon_0 ab}=\displaystyle \int_V \frac{\epsilon_0 \boldsymbol{E}(\boldsymbol{r})^2}{2} dV
$$のような表式で与えられる。
証明 空間の対称性と電荷保存則より、内側の導体表面には一様面密度\(\sigma_0=\frac{Q}{4\pi a^2}\)、導体球殻の導体球と向かい合う側に一様面密度\(-\frac{Q}{4\pi b^2}\)の球対称電荷分布がつくられる。
半径\(R\)の球面上に一様面密度\(\sigma\)で分布した電荷は、球面の内側の電場を打ち消し、電荷合計\(4\pi R^2 \sigma\)がすべて球中心に点電荷として集まったときの電場を球面の外側につくる。導体間につくられる静電場は、内側の導体表面における面電荷と、外側の導体球殻における面電荷がそれぞれ単独で作る静電場の和になるので、これらより直ちに、導体球の中心を原点として極板間のみに\(\boldsymbol{E}(\boldsymbol{r})=\frac{Q}{4\pi \epsilon_0}\frac{\boldsymbol{r}}{r^3}\)の静電場が生じることが示される。電位差は、\(-Q\)の導体球殻から\(+Q\)の導体球へ単位電荷を運ぶときに、静電気力に釣り合わせる外力の仕事を考えると、
$$
\Delta \phi=\displaystyle \int_C \boldsymbol{E}(\boldsymbol{r}) \cdot d \boldsymbol{r} =\displaystyle \int_b^a \frac{Q}{4\pi \epsilon_0 r^2} dr = \frac{Q}{4\pi \epsilon_0}(\frac{1}{a}-\frac{1}{b})
$$となる。平板コンデンサーの電気容量や静電エネルギーは、いま求めた表式と定義に沿って計算すると直ちに示される。□
以上、電気容量やコンデンサーの定義と、その例になります。


コメント