こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。
本稿では、具体的な静電場の現象例として、電気双極子のつくる静電場をみていきます。
電気双極子のつくる静電場
短い間隔をおいて並んだ等しい正負の電荷の対を、電気双極子といいます。例えば、距離\(d\)はなれて並んだ2つの点電荷\(q\)と\(-q\)は電気双極子とみなせ、このとき点電荷\(-q\)からみた点電荷\(q\)の相対位置ベクトルを\(\boldsymbol{d}\)とすると、\(\boldsymbol{p}=q\boldsymbol{d}\)を電気双極子モーメントといいます。電気双極子は同じ大きさ逆符号の2電荷によって、電場や電位が部分的に打ち消され、十分遠方での電場や電位はそのお釣りの項だけが効くために、距離の逆2乗で記述される点電荷の作る電場よりも早く収束しそうだと予想できます。
例3.1(電気双極子のつくる静電場)
間隔を\(d\)だけ離しておかれた、位置\(\frac{\boldsymbol{d}}{2}\)の点電荷\(q\)と位置\(-\frac{\boldsymbol{d}}{2}\)の点電荷\(-q\)を電気双極子とみなしたとき、この2つの点電荷から十分遠方の位置\(\boldsymbol{r}\)における静電場\(\boldsymbol{E}(\boldsymbol{r})\)と、静電ポテンシャル\(\phi(\boldsymbol{r})\)は、
$$
\boldsymbol{E}(\boldsymbol{r})=\frac{1}{4\pi\epsilon_0}\left( \frac{3(\boldsymbol{r} \cdot \boldsymbol{p})\boldsymbol{r}}{r^5}-\frac{\boldsymbol{p}}{r^3} \right)
$$$$
\phi(\mathbf{r})=\frac{1}{4\pi \epsilon_0}\frac{\boldsymbol{r} \cdot \boldsymbol{p}}{r^3}
$$
証明 クーロンの法則と重ね合わせの原理より、任意の位置\(\mathbf{r}\)における静電場\(\boldsymbol{E}(\boldsymbol{r})\)は、
$$
\boldsymbol{E}(\boldsymbol{r})=\frac{q}{4\pi \epsilon_0}\frac{\boldsymbol{r}-\frac{\boldsymbol{d}}{2}}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}+\frac{-q}{4\pi \epsilon_0}\frac{\boldsymbol{r}+\frac{\boldsymbol{d}}{2}}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|^3} = \boldsymbol{r} \left\{ \frac{q}{4\pi \epsilon_0}\left( \frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}-\frac{1}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|^3}\right) \right\} – \frac{\boldsymbol{d}}{2} \left\{ \frac{q}{4\pi \epsilon_0} \left( \frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}+\frac{1}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|^3} \right) \right\}
$$ここで、電気双極子の間隔に比べて位置\(\boldsymbol{r}\)が十分遠方という仮定から、\(\frac{d}{r}\ll 1\)であるとして近似すると、
$$
\frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}= \left| \boldsymbol{r}-\frac{\boldsymbol{d}}{2} \right| ^{-3} = \left\{ \left(\boldsymbol{r}-\frac{\boldsymbol{d}}{2}\right) \cdot \left(\boldsymbol{r}-\frac{\boldsymbol{d}}{2} \right) \right\} ^{-\frac{3}{2}} = \left\{ r^2- \boldsymbol{r}\cdot \boldsymbol{d}+\frac{d^2}{4} \right\} ^{-\frac{3}{2}} = (r^2)^{-\frac{3}{2}} \left\{ 1-\frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2}+\frac{1}{4} \left(\frac{d}{r}\right)^2 \right\} ^{-\frac{3}{2}} \simeq r^{-3} \left\{ 1-\frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\} ^{-\frac{3}{2}} \simeq \frac{1}{r^3} \left\{ 1+\frac{3}{2} \frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\}
$$となる。ただし、はじめの近似は微小項の2次以上を切り捨て、次の近似ではマクローリン展開に由来する近似式である、\(|x|\ll 1\)のとき実数\(p\)に対し\((1+x)^p \simeq 1+px\)を用いている。同様にして、
$$
\frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|^3}\simeq \frac{1}{r^3} \left\{ 1-\frac{3}{2} \frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\}
$$であるので、これらを用いると静電場の表式は、
$$
\boldsymbol{E}(\boldsymbol{r}) \simeq \boldsymbol{r} \left\{ \frac{q}{4\pi \epsilon_0} \frac{1}{r^3} \frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\} – \frac{\boldsymbol{d}}{2} \left\{ \frac{q}{4\pi \epsilon_0}\frac{2}{r^3} \right\} = \frac{1}{4\pi \epsilon_0} \left\{ \frac{3(\boldsymbol{r}\cdot \boldsymbol{p})\boldsymbol{r}}{r^5}-\frac{\boldsymbol{p}}{r^3} \right\}
$$として示される。同様にクーロンの法則と重ね合わせの原理より、位置\(\boldsymbol{r}\)における電位\(\phi(\boldsymbol{r})\)は、
$$
\phi(\boldsymbol{r})=\frac{q}{4\pi \epsilon_0}\frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|}+\frac{-q}{4\pi \epsilon_0}\frac{1}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|}
$$ここで、電気双極子の間隔に比べて位置\(\boldsymbol{r}\)が十分遠方にあるという仮定から、\(\frac{d}{r}\ll 1\)であるとして同様に近似すると、
$$
\frac{1}{|\boldsymbol{r}-\frac{\boldsymbol{d}}{2}|}\simeq \frac{1}{r} \left\{ 1+\frac{1}{2} \frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\}
$$$$
\frac{1}{|\boldsymbol{r}+\frac{\boldsymbol{d}}{2}|}\simeq \frac{1}{r} \left\{ 1-\frac{1}{2} \frac{\boldsymbol{r}\cdot \boldsymbol{d}}{r^2} \right\}
$$であるので、これらを用いると静電ポテンシャルの表式は、
$$
\phi(\boldsymbol{r})=\frac{q}{4\pi \epsilon_0}\frac{\boldsymbol{r} \cdot \boldsymbol{p}}{r^3}
$$として示される。□
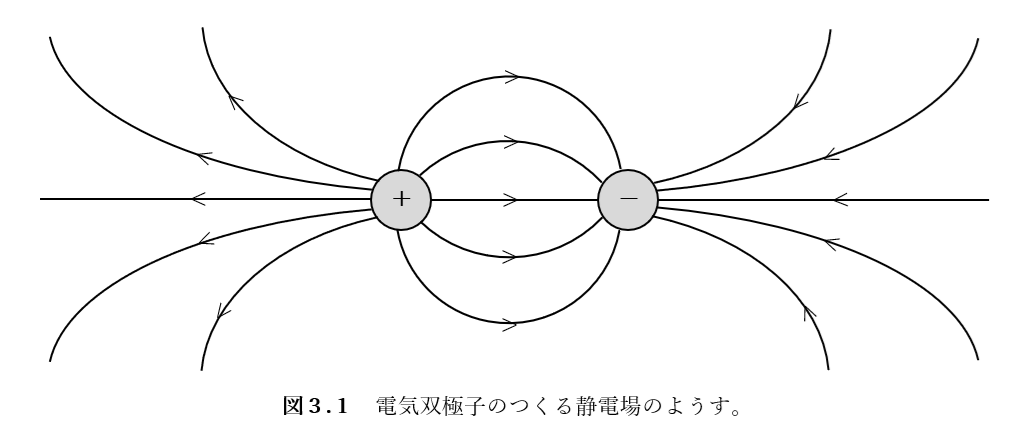
以上、電気双極子のつくる静電場になります。


コメント