【静電場の現象】導体がある空間における静電場

こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

本稿では、導体がある空間における静電場の現象について例をあげてみていきます。

導体がある空間における静電場

導体がある空間における静電場については、導体内部の静電場は０であるとしてすでに分かっていますから、問題になってくるのは導体外部の真空領域における電場$\boldsymbol{E}(\boldsymbol{r})$と、導体表面の電荷面密度$\sigma(\boldsymbol{r})$です。あまりに複雑な状況は課されませんから、よく方法論として試されるのは次の２つが多いです。

導体の存在する空間における静電場を求める方法論１
導体や導体外部の対称性がよいときは、対称性から導体表面の電荷面密度$\sigma(\boldsymbol{r})$が求まる。このときはいままでと同じように、電荷分布から好みの方法で、導体外部の真空領域における静電場$\boldsymbol{E}(\boldsymbol{r})$を求められる。

例として、半径$R$の導体球に電荷$q$を与えたときを考えてみましょう。

電荷を帯びた導体球のつくる静電場
半径$R$の導体球に電荷$q$を与えたとき、電荷分布が落ち着いたときの導体球表面の電荷面密度は
$$
\sigma(\boldsymbol{r})=\frac{q}{4\pi R^2}
$$導体外部の真空領域における静電場は
$$
\boldsymbol{E}(\boldsymbol{r})=\frac{q}{4\pi\epsilon_0}\frac{\boldsymbol{r}}{r^2}\quad(r>R)
$$

証明　導体球表面の電荷面密度は、空間の対称性より明らかである。球対称電荷分布が形成されているとき、位置$\boldsymbol{r}$における電場$\boldsymbol{E}(\boldsymbol{r})$は、半径$r$より内側の球領域の電荷合計がすべて原点に点電荷として集まったときの静電場と等しいから、導体外部の真空領域における静電場は導体球中心に電荷$q$が集まったときの静電場と等しい。よってたしかに、
$$
\boldsymbol{E}(\boldsymbol{r})=\frac{q}{4\pi\epsilon_0}\frac{\boldsymbol{r}}{r^2}\quad(r>R)
$$となり、示された。□

一方で対称性が悪く、導体表面の電荷面密度$\sigma(\boldsymbol{r})$がわからないときは以下を考えます。

導体の存在する空間における静電場を求める方法論２
導体をおくはずの領域に、導体外部の領域における電荷分布と境界条件が同じであるような仮想電荷を導入する。

例として、図１のように無限に広い接地した導体平板に対し、導体外部の領域のある位置に点電荷を置く場合を考えてみましょう。

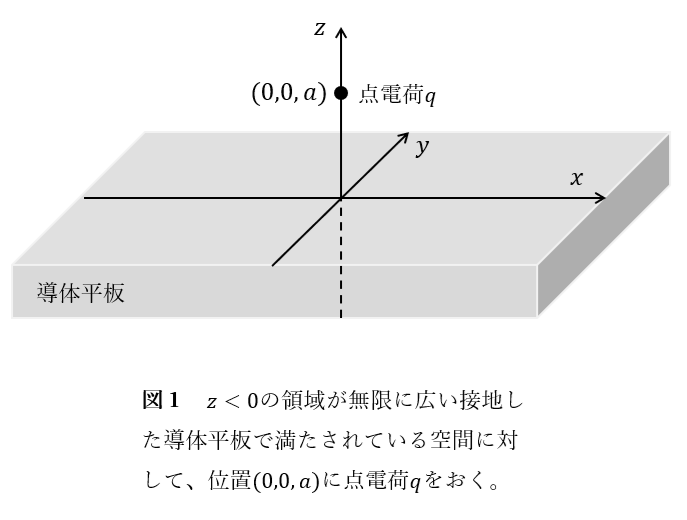
接地した導体平板に正対する点電荷のつくる静電場
$z<0$の領域が導体で満たされている空間に対して、位置$(0,0,a)$に点電荷$q$をおいたとき、電荷分布が落ち着いたときの導体球表面の電荷面密度は
$$
\sigma(\boldsymbol{r})=-\frac{aq}{2\pi (r^2+a^2)^{\frac{3}{2}}}
$$導体外部の真空領域における静電場は
$$
\boldsymbol{E}(x,y,z)=
\begin{pmatrix}
\frac{q}{4\pi \epsilon_0} \left\{ \frac{x}{\{x^2+y^2+(z-a)^2\}^{\frac{3}{2}}} – \frac{x}{\{x^2+y^2+(z+a)^2\}^{\frac{3}{2}}} \right\} \\
\frac{q}{4\pi \epsilon_0} \left\{ \frac{y}{\{x^2+y^2+(z-a)^2\}^{\frac{3}{2}}} – \frac{y}{\{x^2+y^2+(z+a)^2\}^{\frac{3}{2}}} \right\} \\
\frac{q}{4\pi \epsilon_0} \left\{ \frac{z-a}{\{x^2+y^2+(z-a)^2\}^{\frac{3}{2}}} – \frac{z+a}{\{x^2+y^2+(z+a)^2\}^{\frac{3}{2}}} \right\}
\end{pmatrix}
$$

証明　$z<0$の領域が導体で満たされている空間に対して、位置$(0,0,a)$に点電荷$q$をおいたときの、$z \ge 0$の領域につくられる静電場を$\boldsymbol{E}_1(\boldsymbol{r})$とする。また、分極の生じない自由空間中で、位置$(0,0,a)$に点電荷$q$を、位置$(0,0,-a)$に点電荷$-q$をおいたときの、$z \ge 0$の領域につくられる静電場を$\boldsymbol{E}_2(\boldsymbol{r})$とする。
この２つの状況においては、$z \ge 0$の領域における電荷分布は等しく、無限遠と平面$z=0$において電位$\phi(\boldsymbol{r})=0$であるようにとれるから境界条件も等しいので、$\boldsymbol{E}_1(\boldsymbol{r})=\boldsymbol{E}_2(\boldsymbol{r})$が成立している。

よって、導体外部の真空領域における静電場は、分極の生じない自由空間中で、位置$(0,0,a)$に点電荷$q$を、位置$(0,0,-a)$に点電荷$-q$をおいたときの、$z \ge 0$の領域につくられる静電場なので、クーロンの法則よりたしかに、
$$
\boldsymbol{E}(x,y,z)=
\begin{pmatrix}
\frac{q}{4\pi \epsilon_0} \left\{ \frac{x}{\{x^2+y^2+(z-a)^2\}^{\frac{3}{2}}} – \frac{x}{\{x^2+y^2+(z+a)^2\}^{\frac{3}{2}}} \right\} \\
\frac{q}{4\pi \epsilon_0} \left\{ \frac{y}{\{x^2+y^2+(z-a)^2\}^{\frac{3}{2}}} – \frac{y}{\{x^2+y^2+(z+a)^2\}^{\frac{3}{2}}} \right\} \\
\frac{q}{4\pi \epsilon_0} \left\{ \frac{z-a}{\{x^2+y^2+(z-a)^2\}^{\frac{3}{2}}} – \frac{z+a}{\{x^2+y^2+(z+a)^2\}^{\frac{3}{2}}} \right\}
\end{pmatrix}
$$導体表面における電荷面密度を$\sigma(\boldsymbol{r})$、導体表面における電場を$\boldsymbol{E}(\boldsymbol{r})$としたとき、$\sigma(\boldsymbol{r})=\epsilon_0 E(\boldsymbol{r})$でかけるので、
$$
\sigma(\boldsymbol{r})=\epsilon_0
\left| \begin{pmatrix}
\frac{q}{4\pi \epsilon_0} \left\{ \frac{x}{\{r^2+a^2\}^{\frac{3}{2}}} – \frac{x}{\{r^2+a^2\}^{\frac{3}{2}}} \right\} \\
\frac{q}{4\pi \epsilon_0} \left\{ \frac{y}{\{r^2+a^2\}^{\frac{3}{2}}} – \frac{y}{\{r^2+a^2\}^{\frac{3}{2}}} \right\} \\
\frac{q}{4\pi \epsilon_0} \left\{ \frac{-a}{\{r^2+a^2\}^{\frac{3}{2}}} – \frac{a}{\{r^2+a^2\}^{\frac{3}{2}}} \right\}
\end{pmatrix} \right|
=-\frac{aq}{2\pi (r^2+a^2)^{\frac{3}{2}}}
$$である。これで示された。□

以上、導体がある空間における静電場の現象例になります。