静電場における渦なしの法則

こんにちは、turtleです。現在電磁気を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

静電場におけるガウスの法則は、静電場は渦を巻いて回転することがないという法則で、静電場の基本法則の一つでもあります。

積分形の渦なしの法則

積分形の渦なしの法則
任意の閉曲線\(C\)をとるとき、以下が成立する。
$$
\oint_C \boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r}=0
$$

これを示すために補題としてまず以下のことを示します。

補題１
点電荷\(q\),\(q’\)のみが存在する空間において、点電荷\(q\)を固定して、点電荷\(q’\)のみを動かしたときにはたらく静電気力は、保存力(始点と終点さえ定めればその間をどのような経路で運んだとしても釣り合わせる外力のする仕事は一定)である。

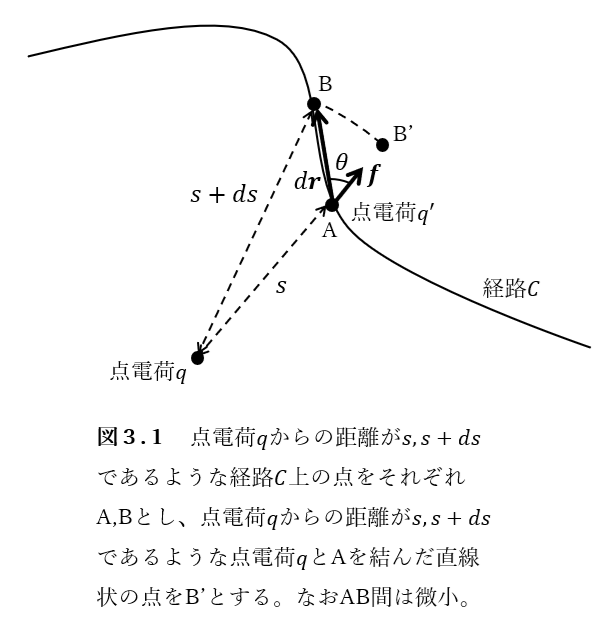
証明　図１のように、点\(A\)、点\(B\)、点\(B’\)を定めるとき、ある経路\(C\)の微小区間、点\(A\)から点\(B\)上で電荷\(q’\)を動かすときの、静電気力のする仕事\(dw\)は、
$$
dw=\mathbf{f}(s) \cdot d\boldsymbol{r}=f(s)dr\cos\theta
$$一方で、微小区間、点\(A\)から点\(B’\)上で電荷\(q’\)を動かすときの、静電気力のする仕事\(dw’\)は、力の向きと移動方向が同じであるため、
$$
dw’={f}(s) ds=f(s)dr\cos\theta \quad (∵ ds=dr \cos\theta)
$$ゆえに任意の経路\(C\)上の、点電荷\(q\)からの距離が\(s\)である点と\(s+ds\)である点を結ぶ微小区間での仕事は、点電荷\(q\)からの距離が\(s\)である任意の点を始点に、点電荷\(q\)からの距離が\(s+ds\)になるまで直線的に離れるような微小経路における仕事と等しい。したがって、十分な長さの経路における仕事は、微小経路における仕事の寄せ集めとみなせるので、任意の経路\(C\)上の、点電荷\(q\)からの距離が\(a\)である点と\(b\)である点を結ぶ経路での仕事は、点電荷\(q\)からの距離が\(a\)である任意の点を始点に、点電荷\(q\)からの距離が\(b\)になるまで直線的に離れるような直線経路における仕事と等しくなる。すなわち、仕事の値は、始点と終点の点電荷からの距離が同じであれば等しいことが示された。□

これより直ちに次のことも成り立ちます。

補題２
任意の電荷分布に対して、静電気力は保存力である。

証明　任意の電荷分布は、微小空間に分けていくと点電荷の集まりとみなせるので、ある電荷分布について点電荷\(q_1\),\(q_2\),…\(q_i\),…の集まりとして扱える。このとき、\(q_1\),\(q_2\),…\(q_i\),…がそれぞれ単独で作る電場を\(\boldsymbol{e}_1\),\(\boldsymbol{e}_2\),…\(\boldsymbol{e}_i\),…とすると、始点\(X\)から終点\(Y\)まで任意の２経路\(C\),\(C’\)で電荷\(q’\)を動かしたときの、静電気力のする仕事は、
$$
\displaystyle \int_{C} q’\boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r} = \displaystyle \int_{C} q’ \left( \sum_i\boldsymbol{e}_i(\boldsymbol{r}) \right) \cdot d\boldsymbol{r} = \sum_i \displaystyle \int_{C} q’\boldsymbol{e}_i(\boldsymbol{r}) \cdot d\boldsymbol{r} = \sum_i \displaystyle \int_{C’} q’\boldsymbol{e}_i(\boldsymbol{r}) \cdot d\boldsymbol{r} = \displaystyle \int_{C’} q’ \left( \sum_i\boldsymbol{e}_i(\boldsymbol{r}) \right) \cdot d\boldsymbol{r} = \displaystyle \int_{C’} q’\boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r}
$$より等しくなる。すなわち、クーロン力は保存力であることが示された。□

示す補題は以上です。ここからすぐに積分形の渦なしの法則が示されます。

証明　クーロン力は保存力であることから、単位電荷に対する始点と終点が等しい経路における仕事\(\oint_C \boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r}\)は、単位電荷を動かさないときの仕事とつねに等しいので、０である。□

微分形の渦なしの法則

物理学の理論が進んでいくにつれ、遠く離れた場所が直接作用しあうのではなく、隣へ隣へと作用が通じて伝わっていくという見方が、より正確な理解を助けることがわかってきました。このすぐ隣同士の局所的な因果関係を記述するものは、積分形に対して微分形と呼ばれることが多いです。
いま紹介した渦なしの法則の記述は、ある閉曲線全体での電場の線積分が０であることを主張したもので、これに対して局所的な位置での回転に関する主張を記述した式は、微分形の渦なしの法則といいます。

微分形の渦なしの法則
以下のように記述する。
$$
\nabla \times \boldsymbol{E}(\boldsymbol{r}) = \mathbf{0}
$$

証明　ある閉曲線を\(C\)、その閉曲線を縁とする任意の曲面を\(S\)として、また、\(\boldsymbol{n}(\boldsymbol{r})\)はこの曲面上の各位置\(\boldsymbol{r}\)での、経路の方向に右ねじを回して進む向きの大きさ1の法線ベクトルを表すこととする。このとき、積分形の渦なしの法則より、
$$
\oint_C \boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r}=0
$$が成り立つ。ここで、左辺はストークスの定理より、
$$
\oint_C \boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r}= \displaystyle \int_S \left( \nabla \times \boldsymbol{E} (\boldsymbol{r}) \right) \cdot \boldsymbol{n}(\boldsymbol{r}) dS
$$と変形できることから、積分形の渦なしの法則は、
$$
\displaystyle \int_S \left( \nabla \times \boldsymbol{E} (\boldsymbol{r}) \right) \cdot \boldsymbol{n}(\boldsymbol{r}) dS =0
$$と書き換えられることがわかる。いま、曲面\(S\)は任意にとれるので、この関係がつねに成り立つには、
$$
\nabla \times \boldsymbol{E} (\boldsymbol{r})=0
$$でなくてはならない。これははじめに与えた表式であるので、これより示された。□

以上、静電場における渦なしの法則の積分形および微分形の記述と、その証明になります。