電磁波

こんにちは、turtleです。現在物理学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

マクスウェル方程式を変形していくと、電荷や電流といった静電場や静磁場の源がない空間でも、電磁場は「波」として空間中を伝わっていくことが分かります。本稿では、電磁波とよばれるこの「波」について見ていきます。

本稿では、電荷や電流といった静電場や静磁場の源がない空間における、現象を考えます。電荷や電流のない空間のことは、電磁気学ではよく真空とよばれます。真空中のマクスウェル方程式は、$\rho,j$がすべての位置で０であるというもとでのマクスウェル方程式なので、以下のようになります。

定理２.４.９(真空中のマクスウェル方程式)
電場$\boldsymbol{E}$、磁場$\boldsymbol{B}$の間に成り立つ、以下の４つの方程式が真空中で成立している。
$$
\nabla \cdot \boldsymbol{E} = 0
$$$$
\nabla \cdot \boldsymbol{B} = 0
$$$$
\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}
$$$$
\nabla \times \boldsymbol{B} = \mu_0 \epsilon_0 \frac{\partial \boldsymbol{E}}{\partial t}
$$ただし、$\epsilon_0$は真空の誘電率、$\mu_0$は真空の透磁率である。

さて、電磁波の数式自体はここから少し計算すると直ちに出てきますよ。ただしこのあと、$\frac{1}{\sqrt{\epsilon_0 \mu_0}}$という式が頻繁に出てきますが、これは表式を重くするため、都合により$c$とおくことにします。

定理２.４.10(電磁波)
定理２.４.９(真空中におけるマクスウェル方程式)の必要十分な解$\boldsymbol{E}(\boldsymbol{r},t)$, $\boldsymbol{B}(\boldsymbol{r},t)$は、以下のようである。
$$
\boldsymbol{E}(\boldsymbol{r},t) = \boldsymbol{E}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]
$$$$
\boldsymbol{B}(\boldsymbol{r},t) = \boldsymbol{B}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]
$$ただし、$\frac{\boldsymbol{k}}{ck} \times \tilde{\boldsymbol{E}}(\boldsymbol{k})= \tilde{\boldsymbol{B}}(\boldsymbol{k})$,　$\boldsymbol{k} \cdot \tilde{\boldsymbol{E}}(\boldsymbol{k}) = \boldsymbol{k} \cdot \tilde{\boldsymbol{B}}(\boldsymbol{k}) = 0$であって、静電場成分$\boldsymbol{E}_0(\boldsymbol{r})$、静磁場成分$\boldsymbol{B}_0(\boldsymbol{r})$は、時間変化しないときのマクスウェル方程式を満たす。

定理２.４.10の証明の前半(十分性の証明)

十分性、つまり定理２.４.10の式で表される場の表式がマクスウェル方程式を満たすことを証明する。
$$
\boldsymbol{E}(\boldsymbol{r},t) = \boldsymbol{E}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]
$$$$
\boldsymbol{B}(\boldsymbol{r},t) = \boldsymbol{B}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]
$$がマクスウェル方程式を満たすことは、その線形性より、$\boldsymbol{E}_0(\boldsymbol{r})$, $Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]$, $\boldsymbol{B}_0(\boldsymbol{r})$, $Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]$がすべてマクスウェル方程式を満たすことと同値である。
ここで、定理２.４.10の仮定より、静電場成分$\boldsymbol{E}_0(\boldsymbol{r})$、静磁場成分$\boldsymbol{B}_0(\boldsymbol{r})$は、時間変化しないときのマクスウェル方程式を満たすとあるので、本証明では$Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]$, $Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]$がマクスウェル方程式を満たすことのみをいえばよい。
さらに線形性より、複素数$\int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}$, $\int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}$がマクスウェル方程式を満たすならば、$Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]$, $Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]$はマクスウェル方程式を自動的に満たすので、証明すべきことは、$\int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}$, $\int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}$がマクスウェル方程式を満たすことである。

第１式について、仮定より、$\boldsymbol{k} \cdot \tilde{\boldsymbol{E}}(\boldsymbol{k}) = 0$であるので、
$$
\nabla \cdot \left( \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right) = \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) \cdot \left( \nabla e^{ i \boldsymbol{k} \cdot \boldsymbol{r} } \right) e^{-ickt} d\boldsymbol{k} = \int_{\boldsymbol{k} \ne \boldsymbol{0}} i \boldsymbol{k} \cdot \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} = 0
$$第２式について、仮定より、$\boldsymbol{k} \cdot \tilde{\boldsymbol{B}}(\boldsymbol{k}) = 0$であるので、全く同様に０になる。
第３式について、左辺と右辺をそれぞれ計算すると、$\frac{\boldsymbol{k}}{ck} \times \tilde{\boldsymbol{E}}(\boldsymbol{k})= \tilde{\boldsymbol{B}}(\boldsymbol{k})$であるので、
$$
\nabla \times \left( \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right) = \int_{\boldsymbol{k} \ne \boldsymbol{0}} \left( \nabla e^{ i \boldsymbol{k} \cdot \boldsymbol{r} } \right) \times \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{-ickt} d\boldsymbol{k} =\int_{\boldsymbol{k} \ne \boldsymbol{0}} i ck \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}
$$$$
-\frac{\partial}{\partial t} \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} = – \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \boldsymbol{k} \cdot \boldsymbol{r} } \left( \frac{\partial}{\partial t} e^{-ickt} \right) d\boldsymbol{k} = \int_{\boldsymbol{k} \ne \boldsymbol{0}} i ck \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}
$$より、左辺と右辺が一致することが分かる。
第４式について、左辺と右辺をそれぞれ計算すると、 $-\tilde{\boldsymbol{E}}(\boldsymbol{k})= c \frac{\boldsymbol{k}}{k} \times \tilde{\boldsymbol{B}}(\boldsymbol{k})$であるので、
$$
\nabla \times \left( \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right) = \int_{\boldsymbol{k} \ne \boldsymbol{0}} \left( \nabla e^{ i \boldsymbol{k} \cdot \boldsymbol{r} } \right) \times \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{-ickt} d\boldsymbol{k} =-\int_{\boldsymbol{k} \ne \boldsymbol{0}} \frac{ik}{c} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}
$$$$
\mu_0 \epsilon_0 \frac{\partial}{\partial t} \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} = \frac{1}{c^2} \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \boldsymbol{k} \cdot \boldsymbol{r} } \left( \frac{\partial}{\partial t} e^{-ickt} \right) d\boldsymbol{k} = -\int_{\boldsymbol{k} \ne \boldsymbol{0}} \frac{ik}{c} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}
$$より、左辺と右辺が一致することが分かる。これより示された。□

定理２.４.10の証明の後半(必要性の証明)

必要性、つまりマクスウェル方程式を満たす解は、すべて必ず定理２.４.10の式で表されることを証明する。任意の物理的に妥当な場$\boldsymbol{E}(\boldsymbol{r}, t)$, $\boldsymbol{B}(\boldsymbol{r},t)$は、空間座標 $\boldsymbol{r}$に関してフーリエ変換可能であるとすると、
$$
\boldsymbol{E}(\boldsymbol{r}, t) = \boldsymbol{E}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \boldsymbol{\mathcal{E}}(\boldsymbol{k}, t) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} d\boldsymbol{k} \right]
$$$$
\boldsymbol{B}(\boldsymbol{r}, t) = \boldsymbol{B}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \boldsymbol{\mathcal{B}}(\boldsymbol{k}, t) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} d\boldsymbol{k} \right]
$$なお、ここでは$\boldsymbol{E}(\boldsymbol{r}, t)$, $\boldsymbol{B}(\boldsymbol{r},t)$の関数形に関してとくに制限しておらず、この表式によって実用上のすべての$\mathbb{R}^3 \to \mathbb{R}^3$の関数形を表すことができ、時間依存性も振幅部分に残されている。
定理２.４.９の第３式の回転をとると、
$$
\nabla \times (\nabla \times \boldsymbol{E}) = -\frac{\partial}{\partial t} (\nabla \times \boldsymbol{B})
$$ベクトル解析の公式$\nabla \times (\nabla \times \boldsymbol{E}) = – \nabla^2 \boldsymbol{E} + \nabla(\nabla \cdot \boldsymbol{E})$と、定理２.４.９の第１式$\nabla \cdot \boldsymbol{E}=0$、第４式$ \nabla \times \boldsymbol{B} = \mu_0 \epsilon_0 \frac{\partial \boldsymbol{E}}{\partial t} $を用いると、以下のようになる。
$$
\nabla^2 \boldsymbol{E} = \frac{1}{c^2} \frac{\partial^2}{\partial t^2}\boldsymbol{E}
$$同様に、定理２.４.９の第４式の回転をとると、
$$
\nabla \times (\nabla \times \boldsymbol{B}) = \frac{1}{c^2} \frac{\partial}{\partial t} (\nabla \times \boldsymbol{E})
$$ベクトル解析の公式$\nabla \times (\nabla \times \boldsymbol{B}) = – \nabla^2 \boldsymbol{B} + \nabla(\nabla \cdot \boldsymbol{B})$と、定理２.４.９の第２式$\nabla \cdot \boldsymbol{B}=0$、第４式$ \nabla \times \boldsymbol{E} = – \frac{\partial \boldsymbol{B}}{\partial t} $を用いると、以下のようになる。
$$
\nabla^2 \boldsymbol{B} = \frac{1}{c^2} \frac{\partial^2}{\partial t^2}\boldsymbol{B}
$$これらに、フーリエ級数展開した$\boldsymbol{E}(\boldsymbol{r}, t)$, $\boldsymbol{B}(\boldsymbol{r},t)$の表式を代入すると、
$$
\nabla^2 \left( \boldsymbol{E}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \boldsymbol{\mathcal{E}}(\boldsymbol{k}, t) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} d\boldsymbol{k} \right] \right) = \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \left( \boldsymbol{E}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \boldsymbol{\mathcal{E}}(\boldsymbol{k}, t) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} d\boldsymbol{k} \right] \right)
$$$$
\nabla^2 \left( \boldsymbol{B}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \boldsymbol{\mathcal{B}}(\boldsymbol{k}, t) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} d\boldsymbol{k} \right] \right) = \frac{1}{c^2} \frac{\partial^2}{\partial t^2} \left( \boldsymbol{B}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \boldsymbol{\mathcal{B}}(\boldsymbol{k}, t) e^{i\boldsymbol{k}\cdot\boldsymbol{r}} d\boldsymbol{k} \right] \right)
$$ここで、時間依存する項としない項は互いに干渉せず、それぞれが個別に方程式を満たさなければならないので、この２式は以下と等価である。
$$
\nabla^2 \boldsymbol{E}_0(\boldsymbol{r}) = \boldsymbol{0}
$$$$
\nabla^2 \boldsymbol{B}_0(\boldsymbol{r}) = \boldsymbol{0}
$$$$
\frac{\partial^2}{\partial t^2} \boldsymbol{\mathcal{E}}(\boldsymbol{k}, t) + c^2 k^2 \boldsymbol{\mathcal{E}}(\boldsymbol{k}, t) = \boldsymbol{0}
$$$$
\frac{\partial^2}{\partial t^2} \boldsymbol{\mathcal{B}}(\boldsymbol{k}, t) + c^2 k^2 \boldsymbol{\mathcal{B}}(\boldsymbol{k}, t) = \boldsymbol{0}
$$下の２つの波動方程式は、角振動数$\omega = ck$の単振動の方程式であるので、これを解くと、
$$
\boldsymbol{\mathcal{E}}(\boldsymbol{k}, t) = \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{-ickt}
$$$$
\boldsymbol{\mathcal{B}}(\boldsymbol{k}, t) = \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{-ickt}
$$となる。ただし、$\tilde{\boldsymbol{E}}(\boldsymbol{k}), \tilde{\boldsymbol{B}}(\boldsymbol{k})$は複素振幅である。つまり、フーリエ級数展開した表式に代入すると、次のようにかけることが、$\boldsymbol{E}(\boldsymbol{r}, t)$, $\boldsymbol{B}(\boldsymbol{r},t)$の必要条件であるとわかる。
$$
\boldsymbol{E}(\boldsymbol{r},t) = \boldsymbol{E}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]
$$$$
\boldsymbol{B}(\boldsymbol{r},t) = \boldsymbol{B}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]
$$
以降は、これがマクスウェル方程式の解になるために必要な条件を考える。
時間依存する項としない項は互いに干渉せず、それぞれが個別に方程式を満たさなければならないので、静電場成分$\boldsymbol{E}_0(\boldsymbol{r})$、静磁場成分$\boldsymbol{B}_0(\boldsymbol{r})$は、時間変化しないときのマクスウェル方程式を満たす必要がある。
時間依存する項について、定理２.４.９(真空中におけるマクスウェル方程式)に順に代入していく。証明の前半と計算自体は被るため、結果のみ書くことにするが、
第１式に代入すると、$i\boldsymbol{k} \cdot \tilde{\boldsymbol{E}}(\boldsymbol{k}) = 0 $すなわち、$\boldsymbol{k} \cdot \tilde{\boldsymbol{E}}(\boldsymbol{k}) = 0$
第２式に代入すると、$i\boldsymbol{k} \cdot \tilde{\boldsymbol{B}}(\boldsymbol{k}) = 0 $すなわち、$\boldsymbol{k} \cdot \tilde{\boldsymbol{B}}(\boldsymbol{k}) = 0$
第３式に代入すると、$\boldsymbol{k} \times \tilde{\boldsymbol{E}}(\boldsymbol{k}) = ck \tilde{\boldsymbol{B}}(\boldsymbol{k})$
第４式に代入すると、$\boldsymbol{k} \times \tilde{\boldsymbol{B}}(\boldsymbol{k}) = – \frac{k}{c} \tilde{\boldsymbol{E}}(\boldsymbol{k})$
を満たしていればよい。したがって、これより示された。□

最後に、定理２.４.10の式が何を表しているか、つまり、真空中の電磁波の特徴を考えます。注意として、電荷や電流といった源がないとき電磁場はいたるところ$\boldsymbol{0}$であるべきだという見方もあるかと思いますが、本定理で考えているのは、宇宙のはじめからあった電磁場、あるいは十分遠くにありすぎて無視できる電荷や電流がつくった電磁場が伝わってきたものとかであると受け取ってもらえれば大丈夫です。

さて、定理２.４.10における解
$$
\boldsymbol{E}(\boldsymbol{r},t) = \boldsymbol{E}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]
$$$$
\boldsymbol{B}(\boldsymbol{r},t) = \boldsymbol{B}_0(\boldsymbol{r}) + Re \left[ \int_{\boldsymbol{k} \ne \boldsymbol{0}} \tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k} \right]
$$について、もちろん、$\boldsymbol{E}_0(\boldsymbol{r})$、$\boldsymbol{B}_0(\boldsymbol{r})$は、静電場や静磁場を表しています。

重要なのは、後ろの時間依存する項ですね。$\tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}$, $\tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}$というのは、波数ベクトル$\boldsymbol{k}$の方向に進行する波を表していて、それをあらゆる$\boldsymbol{k} \ne \boldsymbol{0}$にわたって足し合わせているという表式です。具体的に、表式の各部分について説明すると、以下のようになります。
$\tilde{\boldsymbol{E}}(\boldsymbol{k})$, $\tilde{\boldsymbol{B}}(\boldsymbol{k})$：電場や磁場の$\boldsymbol{k}$近傍の複素振幅の密度
$e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)}$：波数$k$、位相速度$c$の正弦波
$d\boldsymbol{k}$：$\boldsymbol{k}$近傍の微小の範囲の体積
詳しい波動の表式の扱い方は別稿で書きますが、とりあえず$\tilde{\boldsymbol{E}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}$, $\tilde{\boldsymbol{B}}(\boldsymbol{k}) e^{ i \left(\boldsymbol{k} \cdot \boldsymbol{r}-ckt \right)} d\boldsymbol{k}$は、波数ベクトル$\boldsymbol{k}$の方向に進行する、波数$k$、位相速度$c$の正弦波だと納得してください。

さらに、定理２.４.10における条件$\frac{\boldsymbol{k}}{ck} \times \tilde{\boldsymbol{E}}(\boldsymbol{k})= \tilde{\boldsymbol{B}}(\boldsymbol{k})$,　$\boldsymbol{k} \cdot \tilde{\boldsymbol{E}}(\boldsymbol{k}) = \boldsymbol{k} \cdot \tilde{\boldsymbol{B}}(\boldsymbol{k}) = 0$は、どの波数ベクトル$\boldsymbol{k}$に対しても、波数ベクトル$\boldsymbol{k}$の向き、電場の振幅$\tilde{\boldsymbol{E}}(\boldsymbol{k})$の向き、磁場の振幅$\tilde{\boldsymbol{B}}(\boldsymbol{k})$の向きが互いに垂直であることを述べています。

つまり、定理２.４.10の解の時間依存する部分は、どの波数ベクトル$\boldsymbol{k}$に対しても、電場と磁場の波が以下の図２.４.10のようにセットになっていて、これがあらゆる$\boldsymbol{k} \ne \boldsymbol{0}$にわたって足し合わされている、ということです。これを人間は「電磁波」として、社会のさまざまな場面で応用しています。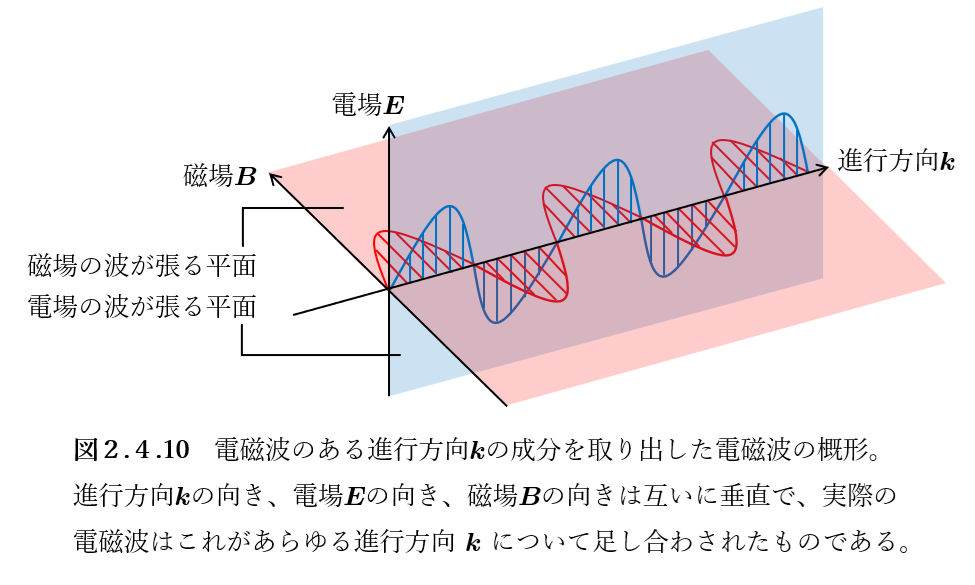

重要なこととして、この波の速度$c=\frac{1}{\sqrt{\epsilon_0 \mu_0}}$について、真空の誘電率と透磁率はいずれもわかっているため、計算してその値を求めることができますが、この値は驚くことに、実験で測定された「光が空気中を進む速度」と非常に近い値になるのです。
このことは、光は電磁波であると結論付けられる１つの根拠になっており、この発見が発展して、反射の法則や屈折の法則などあらゆる光学分野における理論がマクスウェル方程式によって説明されることが分かってから、光学は電磁気学の一分野として吸収されました。