誘電体や磁性体における電磁場

こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

さて親記事では、物質中におけるマクスウェル方程式を導きました。これを再掲します。

定理２.４.Ｍ(物質中のマクスウェル方程式)
誘電体をプラスとマイナスのシートが重なり合ったモデルとみなし、磁性体を微小な電流ループが敷き詰められているモデルとみなしたとき、物質中の電場\(\boldsymbol{E}\)、磁場\(\boldsymbol{B}\)に対し、電束密度\(\boldsymbol{D}\)を\(\boldsymbol{D} = \epsilon_0 \boldsymbol{E} + \boldsymbol{P}\)、磁場の強さ\(\boldsymbol{H}\)を\(\boldsymbol{H} = \frac{1}{\mu_0}\boldsymbol{B} – \boldsymbol{M}\)と定義すると、以下が成立する。
$$
\nabla \cdot \boldsymbol{D} = \rho_f
$$$$
\nabla \cdot \boldsymbol{B} = 0
$$$$
\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}
$$$$
\nabla \times \boldsymbol{H} = \boldsymbol{j}_f + \frac{\partial \boldsymbol{D}}{\partial t}
$$ただし、\(\epsilon_0\)は真空の誘電率、\(\mu_0\)は真空の透磁率、\(\rho_f\)は真電荷密度、\(\boldsymbol{j}_f\)は真電流密度、分極ベクトル\(\boldsymbol{P}\)は電気双極子モーメントの密度、磁化ベクトル\(\boldsymbol{M}\)は磁気双極子モーメントの密度である。

この物質中のマクスウェル方程式は、現実のさまざまな分野で、現象の説明や技術の開発に用いられています。本稿ではその一例として、おそらく読者の皆様もご存じであろう、光がプリズムによって波長ごとに分解される現象について、その説明を試みようと思っています。
光がプリズムによって波長ごとに分解される理由は、高校物理でも扱ったように、波長によって光の絶対屈折率が異なるからでした。ここである波の絶対屈折率は、その波が真空中を進む速度を\(c\)、物質中を進む速度を\(v\)とすると、\(\frac{v}{c}\)でかかれます。\(c\)は定数であるので、\(v\)が光の波長によって異なるはずですから、光がプリズムによって波長ごとに分解される現象を説明するためには、(角振動数は波長の逆数に比例する量であることをふまえると)誘電体中を光が進む速度\(v\)が角振動数に依存することをいえば十分であるということですね。

物質中の光速の角振動数依存性

以上の導入より、本稿でやりたいことは、定理２.４.Ｍを用いて、誘電体中を光が進む速度\(v\)が角振動数に依存することを説明するということです。とはいえ、分子中の電子の運動は、実は量子力学的な効果が重要であるため、いまからモデルを仮定して説明することは、あくまで古典論の範囲でいえることだけであることに注意してください。

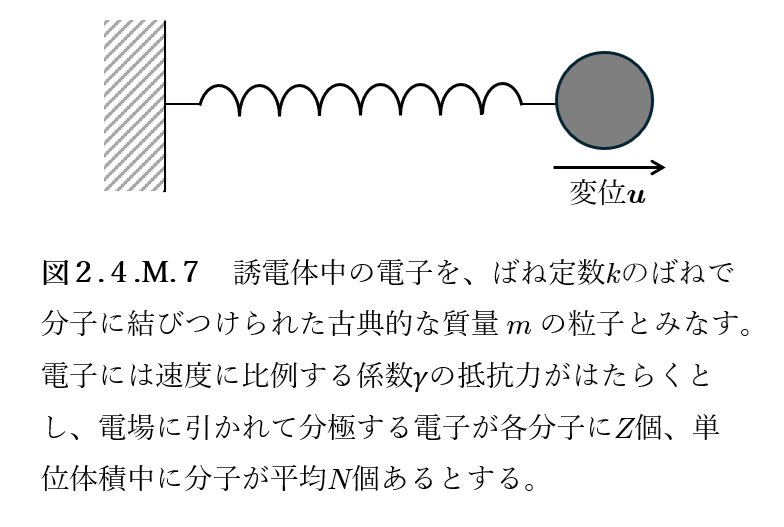
これをよく説明するのは、図２.４.Ｍ.７のような、誘電体中の電子をバネにつながれた質点とみなしたモデルです。これは電子が各分子に束縛されている状態を表しており、電場に引かれて分極する電子が各分子に\(Z\)個、単位体積中に分子が平均\(N\)個あるとします。
このとき分極ベクトル\(\boldsymbol{P}\)と電場\(\boldsymbol{E}\)の向きが一致するので、定義２.４.Ｇにしたがって、\(\boldsymbol{P}= \chi_e \boldsymbol{E}\)なる\(\chi_e\)を電気感受率、\(\epsilon= \epsilon_0 + \chi_e\)を誘電率とすると、以下が成り立ちます。

定理２.４.Ｍ.７(ローレンツ振動子モデル)
誘電体中の電子をバネにつながれた質点とみなしたモデルにおいて、質点の質量を\(m\)、電荷を\(-e\)、変位を\(\boldsymbol{u}\)、ばねのばね定数を\(k\)として、質点は電場\(\boldsymbol{E}\)からのクーロン力\(-e \boldsymbol{E}\)、変位に比例する復元力\(-k \boldsymbol{u}\)、速度に比例する抵抗力\(-\gamma \frac{d \boldsymbol{u}}{dt}\)を受けるとする。
電場に引かれて分極する電子が各分子に\(Z\)個、誘電体の単位体積中に分子が平均\(N\)個あるとするとき、電場が角振動数\(\omega\)で振動する、つまり、\(\boldsymbol{E}=\boldsymbol{E}_0 \cos (\omega t+\alpha)\)という表式でかけるならば、この誘電体の誘電率\(\epsilon\)は以下のように角振動数\(\omega\)に依存する。
$$
\epsilon(\omega) =\epsilon_0+\frac{\tilde{\boldsymbol{P}}}{\tilde{\boldsymbol{E}}} =\epsilon_0+\frac{NZe^2}{m}\frac{1}{\omega_0^2-\omega^2-i\left(\frac{\gamma}{m}\right)\omega}
$$ただし、\(\epsilon_0\)は真空の誘電率、\(\omega_0\)は\(\sqrt{\frac{k}{m}}\)であるとする。

定理２.４.Ｍ.７の証明

電子のモデルである質点の運動方程式は
$$
m\frac{d^2\boldsymbol{u}}{dt^2}+\gamma \frac{d\boldsymbol{u}}{dt}+k\boldsymbol{u}=-e\boldsymbol{E}
$$であり、\(\omega_0=\sqrt{\frac{k}{m}}\)、\(\boldsymbol{E}(t)=\boldsymbol{E}_0\cos(\omega t+\alpha)\)を代入すると、
$$
m\frac{d^2\boldsymbol{u}}{dt^2}+\gamma \frac{d\boldsymbol{u}}{dt}+m{\omega_0}^2\boldsymbol{u}=-e\boldsymbol{E}_0\cos(\omega t+\alpha)
$$となる。ここで、定常解\(\boldsymbol{u}\)は同じ角振動数\(\omega\)で振動するので、\(\boldsymbol{u}=\boldsymbol{u}_0\cos(\omega t+\beta)\)とかけなくてはならない。
いま、複素表示として\(\tilde{\boldsymbol{E}}=\left( \boldsymbol{E}_0 e^{i\alpha} \right) e^{i \omega t}\)、\(\tilde{\boldsymbol{u}}=\left( \boldsymbol{u}_0 e^{i\beta} \right) e^{i \omega t}\)を導入すると、\(\boldsymbol{E}=Re(\tilde{\boldsymbol{E}})\)、\(\boldsymbol{u}=Re(\tilde{\boldsymbol{u}})\)であるので、
$$
m\frac{d^2 \tilde{\boldsymbol{u}}}{dt^2}+\gamma \frac{d \tilde{\boldsymbol{u}}}{dt}+m{\omega_0}^2 \tilde{\boldsymbol{u}} = -e\tilde{\boldsymbol{E}}
$$を方程式(＊)とすると、方程式(＊)の実部は質点の運動方程式となっている。方程式(＊)は実部と虚部それぞれで独立に成立するので、方程式(＊)を満たす\(\tilde{\boldsymbol{u}}\)があれば、この実部\(Re(\tilde{\boldsymbol{u}})\)が質点の変位を示す解である。
\(\frac{d \tilde{\boldsymbol{u}}}{dt}=Re(-i\omega\tilde{\boldsymbol{u}})\)、\(\frac{d^2 \tilde{\boldsymbol{u}}}{dt^2}=Re(-\omega^2 \tilde{\boldsymbol{u}})\)であることをふまえて、\(\tilde{\boldsymbol{E}}=\left( \boldsymbol{E}_0 e^{i\alpha} \right) e^{i \omega t}\)、\(\tilde{\boldsymbol{u}}=\left( \boldsymbol{u}_0 e^{i\beta} \right) e^{i \omega t}\)を方程式(＊)に代入して、\(e^{-i\omega t}\)で約分すると、
$$
\left( -m\omega^2-i\gamma\omega+k \right) \boldsymbol{u}_0 e^{i\beta} = -e \boldsymbol{E}_0 e^{i\alpha}
$$となる。したがって、以下が得られる。
$$
\boldsymbol{u}_0 e^{i\beta} =-\frac{e}{m} \frac{\boldsymbol{E}_0 e^{i\alpha}}{\omega_0^2-\omega^2 – i \frac{\gamma}{m} \omega}
$$
電子1個の変位\(\boldsymbol{u}\)により生じる双極子モーメントは\(\boldsymbol{p}=-e\boldsymbol{u}\)であり、各分子にそのような電子が\(Z\)個あるので分子1個あたりの双極子モーメント\(\boldsymbol{p}_{mol}\)は、\(\boldsymbol{p}_{mol}=Z\boldsymbol{p}=-Ze\boldsymbol{u}\)である。単位体積あたりの分子数が\(N\)個だから分極は \(\boldsymbol{P}=N\boldsymbol{p}_{mol}=-NZe \boldsymbol{u}\)となり、複素表示では
\(\tilde{\boldsymbol{P}}=-NZe \tilde{\boldsymbol{u}}\)である。上式の\(\tilde{\boldsymbol{u}}\)を代入して
$$
\tilde{\boldsymbol{P}}
=\frac{NZe^2}{m}\frac{\tilde{\boldsymbol{E}}}{\omega_0^2-\omega^2-i\left(\frac{\gamma}{m}\right)\omega}
$$を得る。複素表示では、\(\tilde{\boldsymbol{D}} = \epsilon_0 \tilde{\boldsymbol{E}} + \tilde{\boldsymbol{P}}\)であり、\(\tilde{\boldsymbol{D}}= \epsilon \tilde{\boldsymbol{E}}\)と定義されているので、以下が得られる。
$$
\epsilon(\omega) =\epsilon_0+\frac{\tilde{\boldsymbol{P}}}{\tilde{\boldsymbol{E}}} =\epsilon_0+\frac{NZe^2}{m}\frac{1}{\omega_0^2-\omega^2-i\left(\frac{\gamma}{m}\right)\omega}
$$□

ここで誘電率は複素数となっていることに気づくでしょう(というよりも、電気感受率\(\chi_e\)が複素数となっています)。電気感受率というのは、\(\boldsymbol{P}= \chi_e \boldsymbol{E}\)を満たす、つまり、電場\(\boldsymbol{E}\)によってどれだけ分極するかという指標であるわけですが、電子は慣性や抵抗を持つので、電場が変動する場合は、分極は明らかにその瞬間の電場だけでは決まらず過去の電場に遅れて応答することになります。
本稿の伝えたいことがブレるのでここでは細かくはふれませんが、誘電率の虚数部は実数場の位相遅れを表現するものということです。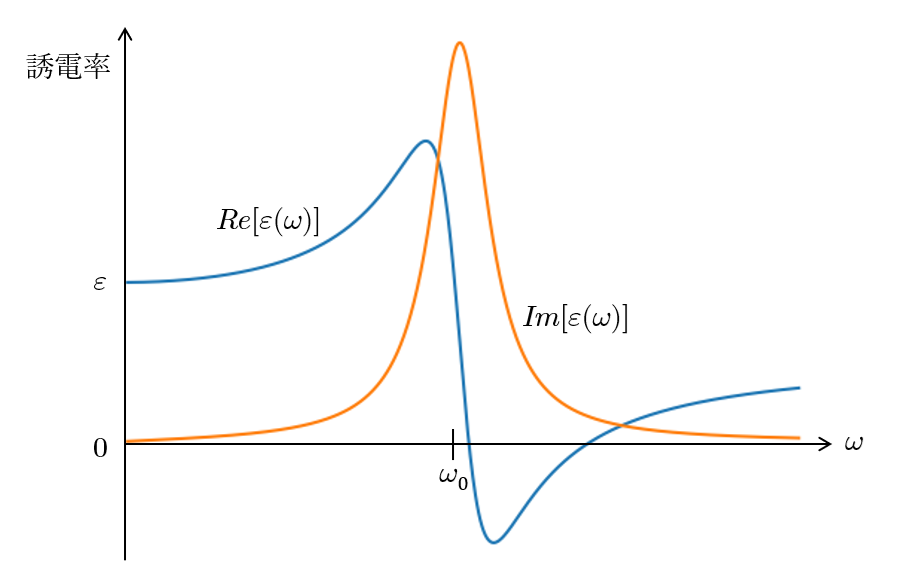

このためグラフを書くと明らかなように、誘電率\(\epsilon(\omega)\)の虚数部は０に収束していきます。したかって、変動があまり早くない振動電場がかかるときには、\(\epsilon(\omega)\)は静電場のときのものを使ってよい、つまり実数部だけで扱ってよいこととします。

さて電場と同様に、簡単のため、いま考えている物質が磁性体としての役割を示すうえで、磁化ベクトル\(\boldsymbol{M}\)と磁場\(\boldsymbol{B}\)の向きが一致するとしたとき、定義２.４.Ｌにしたがって、\(\mu= \mu_0 + \chi_m\)なる\(\mu\)を透磁率と定義できます。
このとき磁場の場合は少し難しいため省略しますが、定理２.４.Ｍ.７と同様に、透磁率が角振動数\(\omega\)に依存すること、変動があまり早くない振動磁場がかかるときには\(\mu(\omega)\)は静磁場のときのものを使ってよいといえることは、想像に難くないでしょう。

さてこうすると、電荷や電流がないときの物質中のマクスウェル方程式は、定理２.４.Ｍより、誘電率\(\epsilon\)と透磁率\(\mu\)を使って、
$$
\nabla \cdot \boldsymbol{E} = 0
$$$$
\nabla \cdot \boldsymbol{B} = 0
$$$$
\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}
$$$$
\nabla \times \boldsymbol{B} = \mu \epsilon \frac{\partial \boldsymbol{E}}{\partial t}
$$とかくことができますが、これは、定理２.４.９(真空中のマクスウェル方程式)の\(\epsilon_0\)を\(\epsilon\)に、\(\mu_0\)を\(\mu\)に対応させたものであるので、この稿の議論の結果より、電磁波の速度は\(v=1/\sqrt{\epsilon \mu}\)とかけるわけです。いま、物体の誘電率\(\epsilon\)や透磁率\(\mu\)は、電磁波の角振動数に依存することがいえているので、これらより明らかに、本稿の目標である、誘電体中を光が進む速度\(v\)が角振動数に依存することがわかりますね。