こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。
さて親記事では、物質中におけるマクスウェル方程式を導きました。これを再掲します。
定理2.4.M(物質中のマクスウェル方程式)
誘電体をプラスとマイナスのシートが重なり合ったモデルとみなし、磁性体を微小な電流ループが敷き詰められているモデルとみなしたとき、物質中の電場\(\boldsymbol{E}\)、磁場\(\boldsymbol{B}\)に対し、電束密度\(\boldsymbol{D}\)を\(\boldsymbol{D} = \epsilon_0 \boldsymbol{E} + \boldsymbol{P}\)、磁場の強さ\(\boldsymbol{H}\)を\(\boldsymbol{H} = \frac{1}{\mu_0}\boldsymbol{B} – \boldsymbol{M}\)と定義すると、以下が成立する。
$$
\nabla \cdot \boldsymbol{D} = \rho_f
$$$$
\nabla \cdot \boldsymbol{B} = 0
$$$$
\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}
$$$$
\nabla \times \boldsymbol{H} = \boldsymbol{j}_f + \frac{\partial \boldsymbol{D}}{\partial t}
$$ただし、\(\epsilon_0\)は真空の誘電率、\(\mu_0\)は真空の透磁率、\(\rho_f\)は真電荷密度、\(\boldsymbol{j}_f\)は真電流密度、分極ベクトル\(\boldsymbol{P}\)は電気双極子モーメントの密度、磁化ベクトル\(\boldsymbol{M}\)は磁気双極子モーメントの密度である。
親記事において、導体中における変動する電磁場は、導体という特別な物質があるわけではなく、 むしろ「誘電体であって磁性体である物質の中に、たまたま束縛されずに自由に動くことができる電荷が混ざっている状態として記述して、その自由に動くことができる電荷がつくる電荷分布や電流分布を真電荷分布や真電流分布と扱う」ということを話しました。
しかし実は、変動する電磁場は、導体中には深く入り込むことができず、導体に侵入しようとした電磁波は非常に早く減衰してしまうことが分かっています。本稿では、これを示します。
オームの法則
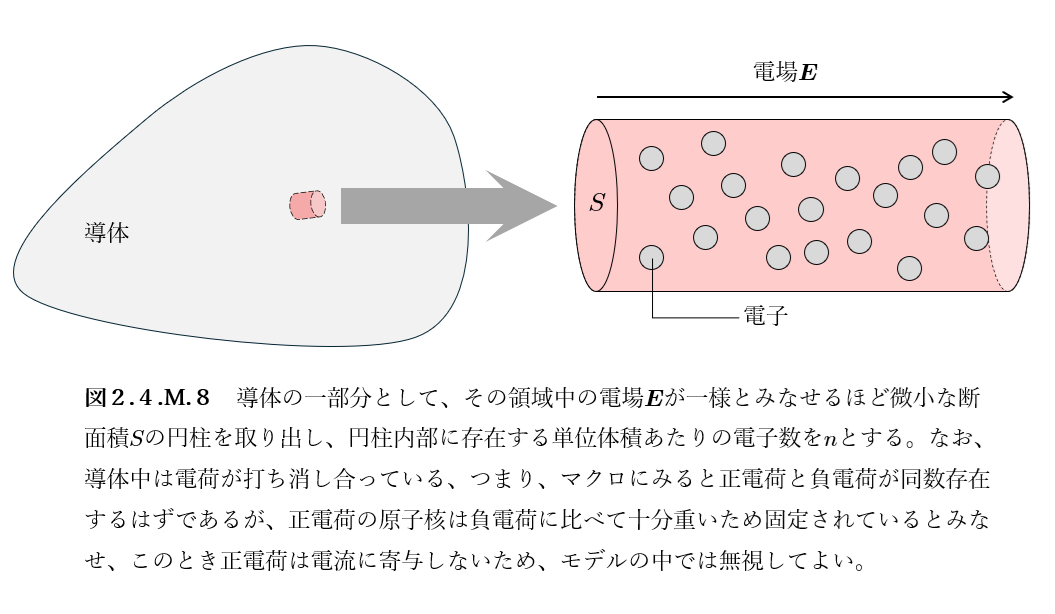
導体中を流れる電流を定量化してよく説明するモデルとして、図2.4.M.8のような導体から取り出した、断面積\(S\)の導体円柱内部に数密度\(n\)で電子が分布している系を考えましょう。このとき、簡単のために、電子が受ける力は、電場\(\boldsymbol{E}\)からのクーロン力\(-e \boldsymbol{E}\)と、分子との衝突などで受ける速度\(\boldsymbol{v}\)比例の抵抗力\(-\alpha \boldsymbol{v}\)であるとします。
さて、導体中の電流をこのようなモデルで説明するとき、次の定理が成り立ち、それらは現実をよく説明しています。
定理2.4.M.9(オームの法則)
導体中の電流が、電場\(\boldsymbol{E}\)からのクーロン力\(-e \boldsymbol{E}\)と、分子との衝突などで受ける速度\(\boldsymbol{v}\)比例の抵抗力\(-\alpha \boldsymbol{v}\)を受けて運動する電子によって生じているとするモデルにおいて、導体中で電子数密度が一様であるとする。このとき、\(\boldsymbol{j}(\boldsymbol{r})\)を位置\(\boldsymbol{r}\)における電流密度とすると、\(\boldsymbol{j}(\boldsymbol{r})=\sigma \boldsymbol{E}(\boldsymbol{r})\)なる導体依存の定数\(\sigma\)が存在する。
定理2.4.M.9の証明
導体内部の電子について、運動方程式を立てると、
$$
m \frac{d \boldsymbol{v}}{dt}=-e \boldsymbol{E} -\alpha \boldsymbol{v}
$$となる。これは\(\boldsymbol{v}\)に関する1階微分方程式であるので、はじめ(\(t=0\))で静止していたとすると、
$$
\boldsymbol{v}=\frac{-e}{\alpha}\boldsymbol{E} \left( 1+e^{-(\alpha/m)t} \right)
$$と表せるため、十分時間がたったとき電子の速度は\((-e/\alpha)\boldsymbol{E}\)に収束する。
一方で、電流\(\boldsymbol{I}\)は、正電荷の流れる方向を向き、単位時間あたりに通過する電荷量を大きさとするベクトル量として定義されるので、電子が単位時間で\(v\)だけ進むことをふまえると、ある断面を単位時間あたりに通過する電子の数は、その断面から電子の進行方向とは逆の向きに距離\(v\)だけ進んだところまでの体積\(Sv\)の円柱に含まれる電子の数\(nSv\)に等しくなる。電流の向きと電子の進む向きは逆であるので、
$$
\boldsymbol{I}=-enS \boldsymbol{v}
$$として表され、電流密度は定義よりこれを\(S\)で割ったものになる。これらの速度と電流の表式から、導体中における電流密度\(\boldsymbol{j}\)は、
$$
\boldsymbol{j}=\frac{ne^2}{\alpha}\boldsymbol{E}
$$と表せる。ここで、\(ne^2/\alpha\)は導体の具体的な構造や温度などによって定まる定数であるので、これを導体依存の定数\(\sigma\)とすると、以下が得られる。
$$
\boldsymbol{j}(\boldsymbol{r})=\sigma \boldsymbol{E}(\boldsymbol{r})
$$□
以上より、導体中の真電流密度は\(\boldsymbol{j}_f(\boldsymbol{r})=\sigma \boldsymbol{E}(\boldsymbol{r})\)と扱うことが一般に許されています。さらに考えている導体において、簡単のために、分極ベクトル\(\boldsymbol{P}\)と電場\(\boldsymbol{E}\)の向きが一致しているとすると、定義2.4.Gにしたがって、誘電率\(\epsilon\)を定義できます。同様に、磁化ベクトル\(\boldsymbol{M}\)と磁場\(\boldsymbol{B}\)の向きが一致しているとすると、定義2.4.Lにしたがって、透磁率\(\mu\)を定義できます。
なお別稿で、電磁場が時間変動するとき、定義に従うと、誘電率\(\epsilon\)や透磁率\(\mu\)は複素数になり、電磁波の角振動数に依存することを話しましたが、ここでは、変動があまり早くない振動電場であるために、誘電率\(\epsilon\)や透磁率\(\mu\)の虚数部や、電磁波の角振動数依存性は無視できることにしましょう。
さて以上のモデル設定より、\(\boldsymbol{j}_f=\sigma \boldsymbol{E}\)、\(\boldsymbol{D}=\epsilon \boldsymbol{E}\)、\(\boldsymbol{H}=\mu \boldsymbol{B}\)を、定理2.4.M(物質中のマクスウェル方程式)に代入すると、以下が成り立ちます。
系2.4.M.10(導体中のマクスウェル方程式)
電場\(\boldsymbol{E}\)、磁場\(\boldsymbol{B}\)に対し、電束密度\(\boldsymbol{D}\)を\(\boldsymbol{D} = \epsilon_0 \boldsymbol{E} + \boldsymbol{P}\)、磁場の強さ\(\boldsymbol{H}\)を\(\boldsymbol{H} = \frac{1}{\mu_0}\boldsymbol{B} – \boldsymbol{M}\)と定義すると、導体中で\(\boldsymbol{j}_f=\sigma \boldsymbol{E}\)、\(\boldsymbol{D}=\epsilon \boldsymbol{E}\)、\(\boldsymbol{H}=\mu \boldsymbol{B}\)なる\(\sigma\)、\(\boldsymbol{D}\)、\(\boldsymbol{H}\)が存在するようなモデルにおいて、
$$
\nabla \cdot \boldsymbol{E} = \frac{\rho_f}{\epsilon}
$$$$
\nabla \cdot \boldsymbol{B} = 0
$$$$
\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}
$$$$
\nabla \times \boldsymbol{B} = \mu \sigma \boldsymbol{E} + \mu \epsilon \frac{\partial \boldsymbol{E}}{\partial t}
$$ただし、\(\epsilon_0\)は真空の誘電率、\(\mu_0\)は真空の透磁率、\(\rho_f\)は真電荷密度、\(\boldsymbol{j}_f\)は真電流密度である。
あとは、ここから出てくる解を計算するだけですね。
導体中の電磁波
以上の系2.4.M.10(導体中のマクスウェル方程式)から、導体中で許される電磁波を求めていきます。簡単のため、真電荷密度\(\rho_f\)はつねにいたるところ0とみなせることとします。
定理2.4.M.11(導体中の電磁波)
系2.4.M.10(導体中のマクスウェル方程式)を満たす電磁場は、\(\rho_f=0\)のもとで以下の方程式を満足する。
$$
\nabla^2 \boldsymbol{E} = \mu \sigma \frac{\partial \boldsymbol{E}}{\partial t} + \mu \epsilon \frac{\partial^2 \boldsymbol{E}}{\partial t^2}
$$$$
\nabla^2 \boldsymbol{B} = \mu \sigma \frac{\partial \boldsymbol{B}}{\partial t} + \mu \epsilon \frac{\partial^2 \boldsymbol{B}}{\partial t^2}
$$
定理2.4.M.11の証明
系2.4.10の第3式の回転をとると、
$$
\nabla \times (\nabla \times \boldsymbol{E}) = -\frac{\partial}{\partial t} (\nabla \times \boldsymbol{B})
$$ベクトル解析の公式\(\nabla \times (\nabla \times \boldsymbol{E}) = – \nabla^2 \boldsymbol{E} + \nabla(\nabla \cdot \boldsymbol{E})\)と、系2.4.10の第1式\(\nabla \cdot \boldsymbol{E}=0\)、第4式\( \nabla \times \boldsymbol{B} = \mu \sigma \boldsymbol{E} + \mu \epsilon \frac{\partial \boldsymbol{E}}{\partial t} \)を用いると、以下のようになる。
$$
\nabla^2 \boldsymbol{E} = \mu \sigma \frac{\partial \boldsymbol{E}}{\partial t} + \mu \epsilon \frac{\partial^2 \boldsymbol{E}}{\partial t^2}
$$同様に、系2.4.10の第4式の回転をとると、
$$
\nabla \times (\nabla \times \boldsymbol{B}) = \nabla \times \left( \mu \sigma \boldsymbol{E} + \mu \epsilon \frac{\partial \boldsymbol{E}}{\partial t} \right) = \mu \sigma (\nabla \times \boldsymbol{E}) + \mu \epsilon \frac{\partial}{\partial t} (\nabla \times \boldsymbol{E})
$$ベクトル解析の公式\(\nabla \times (\nabla \times \boldsymbol{B}) = – \nabla^2 \boldsymbol{B} + \nabla(\nabla \cdot \boldsymbol{B})\)と、定理2.4.9の第2式\(\nabla \cdot \boldsymbol{B}=0\)、第3式\( \nabla \times \boldsymbol{E} = – \frac{\partial \boldsymbol{B}}{\partial t} \)を用いると、以下のようになる。
$$
\nabla^2 \boldsymbol{B} = \mu \sigma \frac{\partial \boldsymbol{B}}{\partial t} + \mu \epsilon \frac{\partial^2 \boldsymbol{B}}{\partial t^2}
$$□
系2.4.M.12
系2.4.M.10(導体中のマクスウェル方程式)を満たす電磁場について、\(\rho_f=0\)のもとで、\(\sigma \gg \epsilon \omega\)が成立する良導体へ侵入した電磁波の振幅は、距離\(\delta=2/\sqrt{\mu \sigma \omega}\)進むと、表面での強さの\(1/e\)(約37%)まで落ち込む。
系2.4.M.12の証明
電磁波が\(z\)軸方向に進む平面波であると仮定して、電場\(\boldsymbol{E}\)と磁場\(\boldsymbol{B}\)を複素表示の実部として以下のように置く。
$$
\boldsymbol{E}(z, t) = Re \left[ \tilde{\boldsymbol{E}}(z, t) \right] =Re \left[ \tilde{\boldsymbol{E}}_0 e^{i(\tilde{k}z – \omega t)} \right]
$$$$
\boldsymbol{B}(z, t) = Re \left[ \tilde{\boldsymbol{B}}(z, t) \right] = Re \left[ \tilde{\boldsymbol{B}}_0 e^{i(\tilde{k}z – \omega t)} \right]
$$ただし、\(\omega\)は角振動数、\(\tilde{k}\)は複素波数(導体中では波数も複素数として扱う)、\(\tilde{\boldsymbol{E}}_0\)と\(\tilde{\boldsymbol{B}}_0\)は複素振幅である。定理2.4.M.11より、電場と磁場は同じ波動方程式を満たすため、これ以降はとくに電場について扱うが、磁場についても同じ議論が成り立つ。
計算すると、\(\nabla^2 \boldsymbol{E}(z, t) = -\tilde{k}^2 \boldsymbol{E}(z, t)\), \(\frac{\partial}{\partial t}\boldsymbol{E}(z, t) = -i\omega \boldsymbol{E}(z, t)\), \(\frac{\partial^2}{\partial t^2}\boldsymbol{E}(z, t) = -\omega^2 \boldsymbol{E}(z, t)\)となるので、これを定理2.4.M.11の第1式に代入すると、
$$
-\tilde{k}^2 \tilde{\boldsymbol{E}}_0 = \mu \sigma (-i\omega) \tilde{\boldsymbol{E}}_0 + \mu \epsilon (-\omega^2) \tilde{\boldsymbol{E}}_0
$$となり、両辺を\(\tilde{\boldsymbol{E}}_0\)で約分して整理すると、複素波数の二乗 \(\tilde{k}^2\)に関する分散関係の式\(\tilde{k}^2 = \mu \epsilon \omega^2 + i \mu \sigma \omega\)が得られる。
\(\tilde{k} = k + i\kappa\)(\(k\), \(\kappa\)は実数)とすると、先の平面波の式に戻して、
$$
\tilde{\boldsymbol{E}(z, t)} = \tilde{\boldsymbol{E}}_0 e^{i((k + i\kappa)z – \omega t)} = \left( \tilde{\boldsymbol{E}}_0 e^{-\kappa z} \right) e^{i(kz – \omega t)}
$$となるので、カッコでくくった部分は波数\(k\)で伝播する波を示す一方、\(e^{-\kappa z}\)の部分は、距離\(z\)が進むにつれて、導体中の電磁波の振幅が指数関数的に減衰していくことを示していることがわかる。電磁波の振幅は\(e^{-\kappa z}\)に従って減衰することから、距離\(z\)が\(\delta = 1/\kappa\)進むと、振幅が表面での値の\(1/e\)になるといえる。
さて、\(\tilde{k}^2 = \mu \epsilon \omega^2 + i \mu \sigma \omega\)とかける一方、\(\tilde{k}^2 = (k + i\kappa)^2 = (k^2 – \kappa^2) + i(2k\kappa)\)であったため、実部と虚部をそれぞれ比較すると、\(k^2 – \kappa^2 = \mu \epsilon \omega^2\), \(2k\kappa = \mu \sigma \omega\)となり、この2式を連立すると以下が得られる。
$$
k = \omega \sqrt{\frac{\mu \epsilon}{2}} \left[ \sqrt{1 + \left(\frac{\sigma}{\epsilon \omega}\right)^2} + 1 \right]^{1/2}
$$$$
\kappa = \omega \sqrt{\frac{\mu \epsilon}{2}} \left[ \sqrt{1 + \left(\frac{\sigma}{\epsilon \omega}\right)^2} – 1 \right]^{1/2}
$$良導体においては導電率\(\sigma\)が非常に大きいため、\(\sigma \gg \epsilon \omega\)が成立するので、この近似を用いると、
$$
\kappa \approx \omega \sqrt{\frac{\mu \epsilon}{2}} \sqrt{\frac{\sigma}{\epsilon \omega}} = \sqrt{\frac{\omega^2 \mu \epsilon \sigma}{2 \epsilon \omega}} = \sqrt{\frac{\omega \mu \sigma}{2}}
$$とかけるから、電磁波の振幅が表面での値の\(1/e\)になる深さ\(\delta\)は、\(1/\kappa = 2/\sqrt{\mu \sigma \omega}\)として示される。□
これで本稿の目的であった、変動する電磁場は導体中には深く入り込むことができず、導体に侵入しようとした電磁波は非常に早く減衰してしまうことを示すことができました。
さて、電磁波の振幅が表面での値の\(1/e\)になる深さ\(\delta\)の表式、\(2/\sqrt{\mu \sigma \omega}\)を見ると、周波数\(f\)が高いほど、導電率\(\sigma\)が高い(より良い導体である)ほど、透磁率\(\mu\)が高い(磁化しやすい)ほど、電磁波は導体の表面しか伝わらず、導体内部には入り込めないことが分かりますね。
実際にどのくらいのスケールかを計算してみましょう。私たちの身の回りで最も一般的な導体である銅を例に挙げて、周波数ごとに計算すると、銅の導電率\(\sigma \approx 5.8 \times 10^7 S/m\)と透磁率\(\mu \approx 4\pi \times 10^{-7} H/m\)を\(\delta = 2/\sqrt{\mu \sigma \omega}\)に代入すると、銅の表皮深さは周波数\(f Hz\)を用いて、おおよそ\(\delta \approx 66/\sqrt{f} mm\) と与えられます。
例えば、家庭用の交流電源(50 Hz/60 Hz)の場合、深さ\(\delta\)は約9.3 mm/約8.5 mmとなる一方、Wi-Fiや電子レンジ(2.4 GHz)の場合は、深さ\(\delta\)はわずか約0.0013 mmとなるわけです。


コメント