【静電場】導体

こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

電磁気現象を考える空間として、これまでは分極の生じない自由空間を用いてきましたが、空間が物質で埋まっていると、電荷分布が同じでも作られる静電場は異なります。空間が分極の生じない自由空間ではないときの静電場の生成のようすは、主に空間が誘電体で埋まっているときと導体で埋まっているときで大きく異なりますが、本稿ではとくに導体のときをみていきます。

導体
導体の存在する空間における静電場
導体表面の電荷面密度

導体

物質には、電気を通しやすいものと通しにくいものがあることが、古くから知られていましたが、このうち電気を通しやすいものを導体とよびます。導体が電気を伝える仕組みは、それを構成する原子の核に束縛されずに、金属の中を自由に動き回ることのできる自由電子にあり、自由電子がわれわれが設定した電荷による電場の影響を受けると、それを打ち消す方向に分布が変化する性質があります。
この自由電子の性質から、以下のことが成り立ちます。

導体の性質１
導体内部のあらゆる位置$\boldsymbol{r}$において、電場$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$

証明　導体内部のある位置$\boldsymbol{r}$において、電場$\boldsymbol{E}(\boldsymbol{r})\ne\boldsymbol{0}$と仮定すると、その電場によって自由電子が動かされるが、これは電荷配置が落ち着いていることに矛盾するので、導体内部のあらゆる位置$\boldsymbol{r}$において、電場$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$である。これで示された。□

導体の性質２
導体内部のあらゆる位置$\boldsymbol{r}$において、電位$\phi(\boldsymbol{r})$は一定である。

証明　導体内部のある位置$\boldsymbol{r}_0$を基準とした、導体内部の別の位置$\boldsymbol{r}$の電位$\phi(\boldsymbol{r})-\phi(\boldsymbol{r}_0)$を求める。定義よりこれは、位置$\boldsymbol{r}_0$から位置$\boldsymbol{r}$へ単位電荷を動かすときの、電気的な力に釣り合わせる外力のする仕事に等しいが、あらゆる位置で単位電荷にはたらく電気的な力は$\boldsymbol{0}$であるから、この仕事も０である。ゆえに$\phi(\boldsymbol{r})-\phi(\boldsymbol{r}_0)=0$より、導体内部のあらゆる位置$\boldsymbol{r}$において、電位$\phi(\boldsymbol{r})$は一定である。これで示された。□

導体の性質３
電荷配置が落ち着いたとき、電荷は導体表面のみに分布している。

証明　電荷配置が落ち着いたときに導体内部にも電荷が分布していると仮定すると、(微分形の)ガウスの法則よりその位置での電場の発散があることになり、先に示した導体内部のあらゆる位置$\boldsymbol{r}$において、電場$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$であることに矛盾するので、電荷は導体表面のみに分布する。これで示された。□

導体の性質４
導体表面における電場は$\boldsymbol{0}$もしくは導体表面に垂直である。

証明　導体表面に沿って単位電荷を微小に$d \boldsymbol{r}$動かしたときに、静電気力につりあわせる外力のする仕事は、-$\boldsymbol{E}(\boldsymbol{r}) \cdot d \boldsymbol{r}$であるが、これは定義より、始点を基準とした終点の電位に等しいため０である。
$\boldsymbol{E}(\boldsymbol{r}) \cdot d \boldsymbol{r}=0$ならば、$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$もしくは$\boldsymbol{E}(\boldsymbol{r}) \perp d \boldsymbol{r}$であるので、これで示された。□

導体の存在する空間における静電場

導体内部の静電場は０であるとしてすでに分かっていますから、問題になってくるのは導体外部の真空領域における電場$\boldsymbol{E}(\boldsymbol{r})$と、導体表面の電荷面密度$\sigma(\boldsymbol{r})$です。あまりに複雑な状況は課されませんから、よく方法論として試されるのは次の２つが多いです。

導体の存在する空間における静電場を求める方法論１
導体や導体外部の対称性がよいときは、対称性から導体表面の電荷面密度$\sigma(\boldsymbol{r})$が求まる。このときはいままでと同じように、電荷分布から好みの方法で、導体外部の真空領域における静電場$\boldsymbol{E}(\boldsymbol{r})$を求められる。

これを使えるのは、例えば、他に電荷のない空間に電荷$q$を帯びた半径$R$の導体球をおいた場合や、平板コンデンサーの両極板に電荷$\pm q$をそれぞれ与えた場合など、対称性がよいために、導体内部の電荷がその導体表面に移動してしまったあとの電荷の状態が計算できるときです。
この電荷面密度さえわかれば、あとはいまわかっている電荷分布が真空領域にあったとしたときにつくるであろう静電場を、クーロンの法則やガウスの法則、ポアソンの方程式など好みの方法で求めることができます。

一方で対称性が悪く、導体表面の電荷面密度$\sigma(\boldsymbol{r})$がわからないときもあるでしょう。ここで、静電場に関する以下の定理を使います。

ある領域内で電荷分布と境界条件が同じであれば、その領域外の電荷分布がどのようであろうと、考えている領域における静電場$\boldsymbol{E}(\boldsymbol{r})$や電位$\phi(\boldsymbol{r})$は等しい。

この定理が使える状況を考えましょう。簡単のために、分極の生じない自由空間におく導体は１つとして、また導体外部の領域における電荷分布を$\rho_0(\boldsymbol{r})$とします。
いま導体で埋まっている領域を仮想的に立体領域$V$として、導体のかわりに立体領域$V$の内部におさまる簡単な電荷分布$\rho_1(\boldsymbol{r})$を考えると、
・$\rho_1(\boldsymbol{r})$のみがつくる電位は、無限遠で０に収束するようにとれる
・$\rho_0(\boldsymbol{r})$のみがつくる電位と、$\rho_1(\boldsymbol{r})$のみがつくる電位の和が、立体領域$V$と外部との境界面上のすべての位置$\boldsymbol{r}$で一定値をとる
の２つを満たしていると仮定します。このとき、電荷分布$\rho_0(\boldsymbol{r})+\rho_1(\boldsymbol{r})$が分極の生じない自由空間中に存在する状況と、立体領域$V$が導体で埋まっていて導体外部の真空領域に電荷分布$\rho_0(\boldsymbol{r})$が存在する状況では、導体外部の領域における電荷分布と境界条件が同じであるため、先に紹介した定理より、静電場$\boldsymbol{E}(\boldsymbol{r})$や電位$\phi(\boldsymbol{r})$も等しいといえます。

導体の存在する空間における静電場を求める方法論２
導体をおくはずの領域に、導体外部の領域における電荷分布と境界条件が同じであるような仮想電荷を導入する。

言葉だけでは理解するのは難しいでしょうから、導体の存在する空間における静電場の求め方については、ぜひ別の記事で紹介する例を通して理解してください。

導体表面の電荷面密度

導体表面の電荷面密度$\sigma(\boldsymbol{r})$について、以下が成り立ちます。

導体表面の電荷面密度
導体表面における電荷面密度を$\sigma(\boldsymbol{r})$、導体表面における電場を$\boldsymbol{E}(\boldsymbol{r})$としたとき、$\sigma(\boldsymbol{r})=\epsilon_0 E(\boldsymbol{r})$

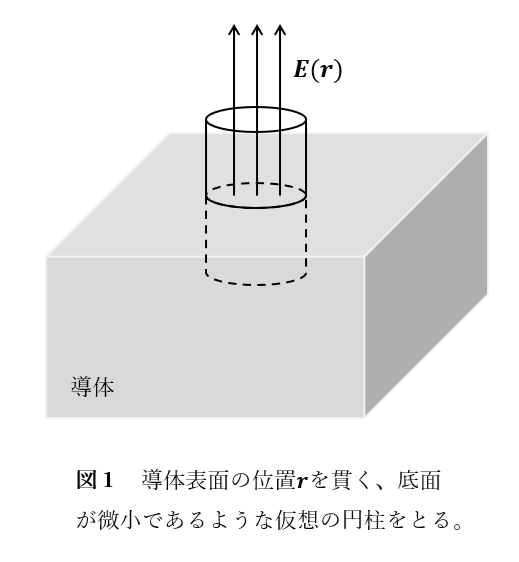
証明　導体表面の位置$\boldsymbol{r}$を貫く、図１のような仮想の円柱に対して積分形のガウスの法則を用いる。この円柱の底面を$\Delta S$とすると、導体表面における電場は$\boldsymbol{0}$もしくは導体表面に垂直であることから、
$$
E(\boldsymbol{r}) \Delta S=\frac{\sigma(\boldsymbol{r}) \Delta S}{\epsilon_0}
$$より、これを変形すると示される。□

以上、電磁気現象における導体のふるまいになります。