こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。
突然ですが「電磁誘導」という現象について、中学や高校で扱ったことがあると思います。具体的には、変化する磁場が導体内に電流を生じさせる現象のことでした。
さて、親記事ではすでに、電磁気学において「何を自明なルール、すなわち原理と認め、そこから何が定理として導かれるか」という論理構造が歴史的に何度も見直されてきたことを述べました。
実はこのことは「電磁誘導」という現象にも大きくかかわっており、古典電磁気学では原因の異なる2つの現象のことをまとめて「電磁誘導」と呼ぶことにしていました。原因は異なるにも関わらず、この2つはあとで述べるように同じ表式で説明することができたため、これは物理学における1つの謎となっていましたが、のちにアインシュタインによってつくられた相対論が導入された後の相対論的電磁気学では実はこの2つが1つの原因に帰結することが示されています。
本稿では、古典電磁気学における電磁誘導、つまり原因の異なる2種類の「変化する磁場が導体内に電流を生じさせる現象」を見ていきます。まず、古典電磁気学において原理とされていた、ローレンツ力の式と、マクスウェル方程式を再掲しておきます。
原理2.3(ローレンツ力の式)
電場\(\boldsymbol{E}\)および磁場\(\boldsymbol{B}\)が存在する空間において、速度\(\boldsymbol{v}\)で運動する電荷\(q\)が受ける力\(\boldsymbol{F}\)は、電気的な力と磁気的な力のベクトル和として、以下で与えられる。
$$
\boldsymbol{F} = q(\boldsymbol{E} + \boldsymbol{v} \times \boldsymbol{B})
$$
原理2.4(マクスウェル方程式)
電場\(\boldsymbol{E}\)、磁場\(\boldsymbol{B}\)、電荷密度\(\rho\)、電流密度\(\boldsymbol{j}\)の間に成り立つ、以下の4つの基礎方程式をマクスウェル方程式と呼ぶ。
$$
\nabla \cdot \boldsymbol{E} = \frac{\rho}{\epsilon_0}
$$$$
\nabla \cdot \boldsymbol{B} = 0
$$$$
\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}
$$$$
\nabla \times \boldsymbol{B} = \mu_0 \boldsymbol{j} + \mu_0 \epsilon_0 \frac{\partial \boldsymbol{E}}{\partial t}
$$ただし、\(\epsilon_0\)は真空の誘電率、\(\mu_0\)は真空の透磁率である。
ローレンツ力に起因する電磁誘導
高校で扱った電磁誘導を振り返ってみると、磁場によって回路に起電力が誘導されるのは
回路が運動したり変形したりする場合
磁場が時間的に変動する場合
の2つがありました。この段落ではまず、「回路が運動したり変形したりする場合」に回路に起電力が誘導される現象を見ていきます。これは、古典電磁気学の原理の1つであるローレンツ力に起因しています。
定理2.4.7
静磁場\(\boldsymbol{B}(\boldsymbol{r})\)中を運動、あるいは変形する回路\(C\)において発生する誘導起電力\(\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r}\) は、回路を貫く磁束\(\Phi=\int_S \boldsymbol{B} \cdot \boldsymbol{n} dS\)の時間変化率の減少分に等しい。
$$
\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r} = -\frac{d}{dt} \displaystyle \int_S \boldsymbol{B} \cdot \boldsymbol{n} dS
$$ただし、閉曲線\(C\)を縁とする任意の曲面を\(S\)とする。
定理2.4.7の証明
回路上のある位置\(\boldsymbol{r}\)で回路に対して静止している(回路にあわせて動いている)単位電荷が受けるローレンツ力\(\boldsymbol{f}(\boldsymbol{r})\)は、その位置における導線の速度を\(\boldsymbol{v}(\boldsymbol{r})\)としたとき、\(\boldsymbol{f}(\boldsymbol{r}) = \boldsymbol{v}(\boldsymbol{r}) \times \boldsymbol{B}(\boldsymbol{r})\)とかける。
ここで、回路\(C\)において発生する誘導起電力\(\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r}\) は、その定義より、単位電荷が回路を一周する際に受ける仕事であるので、
$$
\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r} = \oint_{C} \frac{\boldsymbol{F}}{q} \cdot d\boldsymbol{r} = \oint_{C} (\boldsymbol{v} \times \boldsymbol{B}) \cdot d\boldsymbol{r}
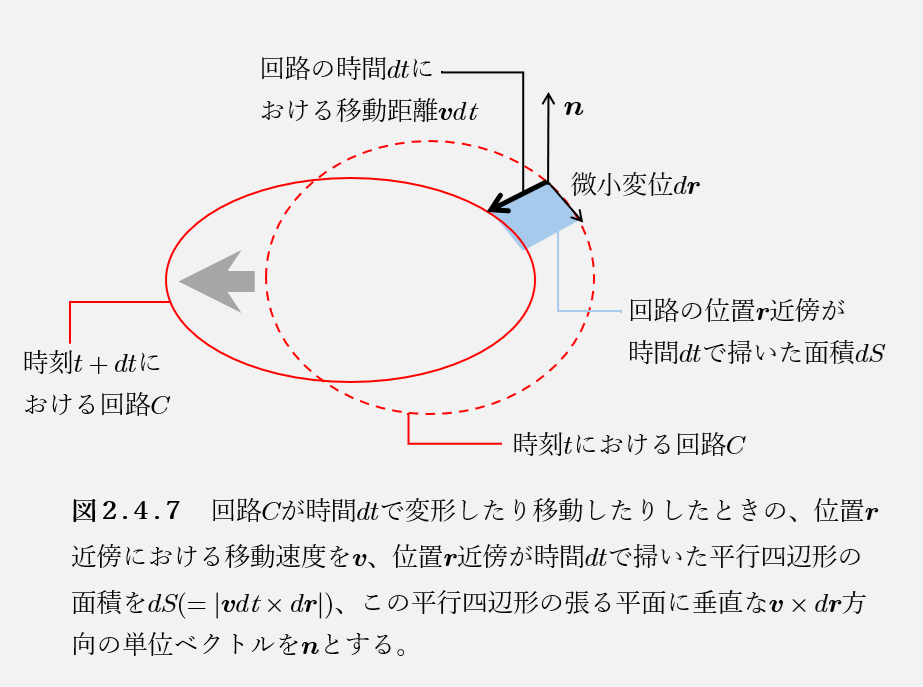
$$とかくことができる。>>スカラー3重積より\((\boldsymbol{v} \times \boldsymbol{B}) \cdot d\boldsymbol{r} = – \boldsymbol{B} \cdot (\boldsymbol{v} \times d\boldsymbol{r})\)となるが、ここで、いま図2.4.7のような関係にあるので、回路の位置\(\boldsymbol{r}\)近傍が時間\(dt\)で掃いた平行四辺形の面積を\(dS\)、この平行四辺形の張る平面に垂直な\(\boldsymbol{v} \times d\boldsymbol{r}\)方向の単位ベクトルを\(\boldsymbol{n}\)とすると、
$$
(\boldsymbol{v} \times \boldsymbol{B}) \cdot d\boldsymbol{r} = – \boldsymbol{B} \cdot (\boldsymbol{v} \times d\boldsymbol{r}) = – \boldsymbol{B} \cdot \boldsymbol{n} \frac{dS}{dt}
$$
これをもとの式に代入すると、以下が得られる。
$$
\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r}=- \oint_{C} \boldsymbol{B} \cdot \boldsymbol{n} \frac{dS}{dt} = \frac{- \oint_{C} \boldsymbol{B} \cdot \boldsymbol{n} {dS}}{dt} = – \frac{d}{dt} \displaystyle \int_S \boldsymbol{B} \cdot \boldsymbol{n} dS
$$□
ファラデーの法則に起因する電磁誘導
続いてこの段落では、「磁場が時間的に変動する場合」に回路に起電力が誘導される現象を見ていきます。これはマクスウェル方程式の第3式\(\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}\)に起因しています。この現象は積分形のマクスウェル方程式をみると直ちにわかるので、定理2.4.3の第3式を再掲しますが、任意の閉曲線\(C\)について、その閉曲線を縁とする任意の曲面を\(S\)とすると、
$$
\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r} = – \displaystyle \int_S \frac{\partial \boldsymbol{B}}{\partial t} \cdot \boldsymbol{n} dS
$$が成立するというものです。さて、実用上の関数では微分と積分を交換できるので、ここでわざと交換操作をしてみると、
$$
\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r} = -\frac{d}{dt} \displaystyle \int_S \boldsymbol{B} \cdot \boldsymbol{n} dS
$$と書くことができますね。この表式は定理2.4.7の式と全く同じことが分かります。
ここで注意をしておきますが、マクスウェル方程式で仮定されている回路\(C\)は静止したものであって、マクスウェル方程式自体は運動したり変形したりする回路についてはとくに何も述べていません。つまり、定理2.4.7の状況はマクスウェル方程式の適用外で、証明にマクスウェル方程式を用いるなんてことは不可能であるわけです。
もちろん、磁場が時間的に変動する場合の電磁誘導をローレンツ力で証明することも不可能です。
ただ、実際に電磁誘導を考える際には、いちいちなにが原因かを考えずに、先の表式で済ませた方が速いときもあるため、高校や工学分野などでは、回路が動いている場合も止まっている場合も含んだ、以下の(広義の)ファラデーの電磁誘導の法則を用いることが多いです。なお、ファラデー自身も実験においてこの2つはとくに区別をしていませんでした。
系2.4.8(広義のファラデーの電磁誘導の法則)
任意の回路\(C\)において、その閉曲線を縁とする任意の曲面を\(S\)、電流の方向に右ねじを回して進む向きの法線ベクトルを\(n\)とすると、回路が運動していようと静止していようと、誘導起電力\(V=\oint_{C} \boldsymbol{E} \cdot d\boldsymbol{r}\)および、磁束\(\Phi=\int_S \boldsymbol{B} \cdot \boldsymbol{n} dS\)を定義することができる。このとき、以下が成立する。
$$
V=-\frac{d \Phi}{dt}
$$
2つの現象が同じ表式で説明する理由が説明されるのは、相対論的電磁気学の完成以後になります。


コメント