古典電磁気学における物質中の電磁場

こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。

親記事やその多くの子記事で考えていたのは、分極や磁化などの生じない自由空間中の電磁場でした。自由空間というのは、空間中に原子や分子がない、つまり電磁気学として純粋に私たちが設定した電荷や電流以外に、電荷や電流が生まれる術がないという空間です。それに対して、本稿では、より現実に即した空間中に原子や分子がある物質中の電磁場を考えていきます。

重要な考え方として、物質中の電磁場も「物質中に生じる原子や分子がつくる電荷や電流をすべて計算することができる」ならば、電荷分布$\rho$を「はじめに設定した電荷と物質中に生じる原子や分子がつくる電荷の和」、電流分布$\boldsymbol{j}$を「はじめに設定した電流と物質中に生じる原子や分子がつくる電流の和」として、原理２.４のマクスウェル方程式で電磁場を計算することができます。
物質中の電磁場については特別で、マクスウェル方程式が成り立たないとかいうわけではありません。物質中の原子や分子をすべて計算するのは現実的に不可能であるため、マクスウェル方程式に必要な、電荷分布$\rho$や電流分布$\boldsymbol{j}$を求めることができないのが問題というわけです。

では、原子や分子をすべて計算し尽くすことは不可能であるので、代わりに、現実の物質をよく説明するモデルを考えます。このモデルをもとに、物質中の静電場と静磁場、そして変動する電磁場を考えていきましょう。

物質中の静電場と静磁場
物質中の変動する電磁場

物質中の静電場と静磁場

現実にはさまざまな物質があり、かなり特殊な現象を生ずる物質などもあるため、本稿ですべてのパターンについてモデルをあげて説明することはできません。ただ、一般に電磁気学を学ぶにあたって、身の回りにある一般の物質を説明するために必要であるのは、誘電体、磁性体、導体の３つのモデルのみです。というのは、身の回りにある一般の物質は、電気的には誘電体あるいは導体に分類され、磁気的には磁性体として扱われるためです。
導体は電気を通す性質を持ち、電流を流す役割をします。
誘電体は絶縁体ともよばれ、電気を通さない性質を持ち、電場を弱める役割をします。
磁性体は磁石につく性質を持ち、磁場を強める/弱める役割をします。
では、順にみていくことにします。まずこの段落では、物質中の静電場と静磁場を扱います。

導体における静電場

導体をもっともよく説明するのは、プラスの電気を持った重い原子核が、規則正しくビッシリ並んで固定されていて、その隙間をマイナスの電気を持った電子が、特定の原子には縛られずに飛び回っているというモデルです。
導体をこのようなモデルであるとみなすとき、以下の定理が成り立ち、それらは現実をよく説明しています。

定理２.４.Ａ
導体を、プラスの電気を持った重い原子核が、規則正しくビッシリ並んで固定されていて、その隙間をマイナスの電気を持った電子が、特定の原子には縛られずに飛び回っているというモデルとみなしたとき、導体内部のあらゆる位置$\boldsymbol{r}$において、静電場$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$

定理２.４.Ａの証明

導体内部のある位置$\boldsymbol{r}$において、電場$\boldsymbol{E}(\boldsymbol{r})\ne\boldsymbol{0}$と仮定すると、その電場によって自由電子が動かされるが、これは電荷配置が落ち着いていることに矛盾するので、導体内部のあらゆる位置$\boldsymbol{r}$において、電場$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$である。これで示された。□

定理２.４.Ｂ
導体を、プラスの電気を持った重い原子核が、規則正しくビッシリ並んで固定されていて、その隙間をマイナスの電気を持った電子が、特定の原子には縛られずに飛び回っているというモデルとみなしたとき、電荷配置が落ち着いたならば電荷は導体表面のみに分布しており、導体表面における電場は$\boldsymbol{0}$もしくは導体表面に垂直である。

系２.４.Ｂの証明

電荷配置が落ち着いたときに導体内部にも電荷が分布していると仮定すると、(微分形の)ガウスの法則よりその位置での電場の発散があることになり、先に示した導体内部のあらゆる位置$\boldsymbol{r}$において、電場$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$であることに矛盾するので、電荷は導体表面のみに分布する。
また、導体表面に沿って単位電荷を微小に$d \boldsymbol{r}$動かしたときに、静電気力につりあわせる外力のする仕事は、-$\boldsymbol{E}(\boldsymbol{r}) \cdot d \boldsymbol{r}$であるが、これは定義より、始点を基準とした終点の電位に等しいため０である。
$\boldsymbol{E}(\boldsymbol{r}) \cdot d \boldsymbol{r}=0$ならば、$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$もしくは$\boldsymbol{E}(\boldsymbol{r}) \perp d \boldsymbol{r}$であるので、これで示された。□

以上より、導体における静電場は、導体内部のあらゆる位置$\boldsymbol{r}$において、静電場$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$となります。
導体の境界条件については別稿で扱っています。
＞＞導体における境界条件と静電場

誘電体における静電場

導体内部では電子が原子から離れて自由に動き回ることができたのに対して、誘電体内部では電子は原子や分子に縛り付けられていて離れることができないため、原子や分子は電気的中性を保っています。一方で、電子は原子や分子の内部であれば電場にひかれて移動して電気双極子を構成することができるため、マクロに見たとき誘電体に電場をかけるとそれにしたがって電気双極子モーメントが現れることになります。
誘電体の分極によって生じる、物質から取り出すことができない電荷を分極電荷といい、分極電荷の物質全体における和は必ず０になります。なお、分極電荷に対して、これまで扱ってきた取り出すことができる電荷を真電荷といいます。

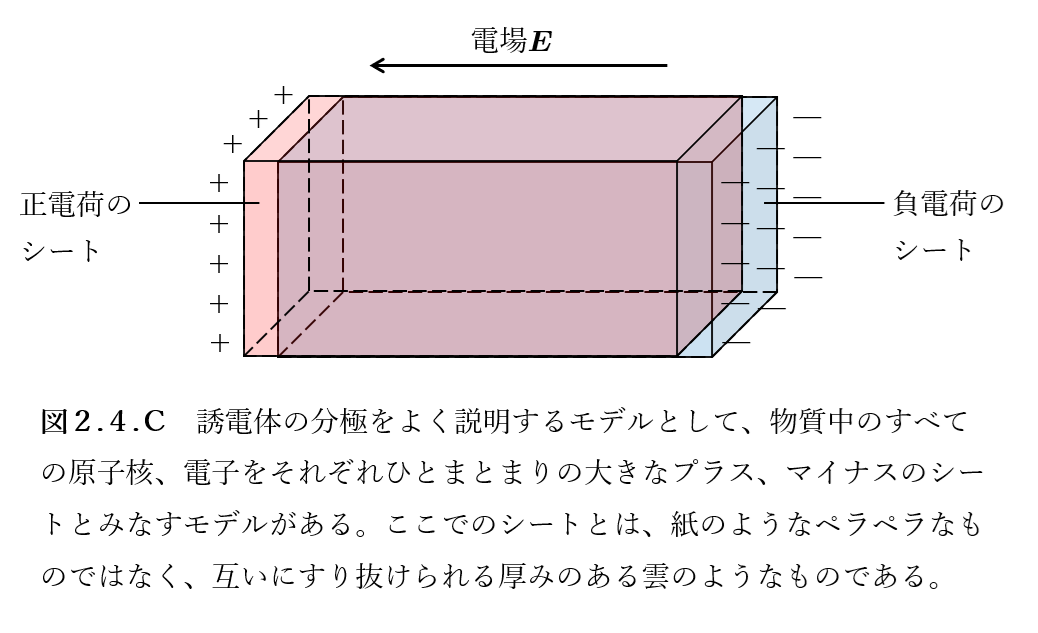
誘電体をマクロでよく説明するのは、図２.４.Ｃのような、物質中のすべての原子核、電子をそれぞれひとまとまりの大きなプラス、マイナスのシート(雲)とみなすモデルです。というのは、電場がかかっておらず電気的中性のときは、プラスのシートとマイナスのシートが完全に重なってどこをとってもプラスとマイナスが打ち消し合っているのに対して、外から電場をかけると、プラスのシートは電場の方向、マイナスのシートは逆方向へ微小にズレることで誘電体の表面に分極表面電荷が現れるという、誘電体の性質をうまく表しているからです。

注意として、正電荷のシートと負電荷のシートは重なると電荷０になりますが、それぞれのシート自体は全体で均一な電荷分布をもつわけではないため、微小にズレることで誘電体の内部にも分極体積電荷が現れることになります。さて、誘電体をこのようなモデルであるとみなすとき、以下の定理が成り立ち、それらは現実をよく説明しています。

定理２.４.Ｃ(分極表面電荷密度)
誘電体をプラスとマイナスのシートが重なり合ったモデルとみなしたとき、誘電体表面のある位置$\boldsymbol{r}$における分極表面電荷密度を$\sigma_p(\boldsymbol{r})$とすると、
$$
\sigma_p(\boldsymbol{r}) = \boldsymbol{P}(\boldsymbol{r}) \cdot \boldsymbol{n}(\boldsymbol{r})
$$となる。ただし、分極ベクトル$\boldsymbol{P}(\boldsymbol{r})$は、位置$\boldsymbol{r}$における電場によって生じた電気双極子モーメントの密度、法線ベクトル$\boldsymbol{n}(\boldsymbol{r})$は、誘電体表面に垂直な単位ベクトルである。

定理２.４.Ｃの証明

定理２.４.Ｄ(分極体積電荷密度)
誘電体をプラスとマイナスのシートが重なり合ったモデルとみなしたとき、誘電体内部のある位置$\boldsymbol{r}$における分極体積電荷密度を$\rho_p(\boldsymbol{r})$とすると、
$$
\rho_p(\boldsymbol{r}) = – \nabla \cdot \boldsymbol{P}(\boldsymbol{r})
$$となる。ただし、分極ベクトル$\boldsymbol{P}(\boldsymbol{r})$は、位置$\boldsymbol{r}$における電場によって生じた電気双極子モーメントの密度である。

定理２.４.Ｄの証明

誘電体はもともと電気的に中性であるため、正電荷のシートの電荷密度を$\rho(\boldsymbol{r})$とすると、負電荷のシートの電荷密度は$- \rho(\boldsymbol{r})$とかける。ここに、電場$\boldsymbol{E}$がかかると、正電荷のシートを微小$\boldsymbol{\delta}_+$、負電荷のシートを微小$\boldsymbol{\delta}_-$変位させることを考え、その相対変位(ズレ)を $\boldsymbol{\delta} = \boldsymbol{\delta}_+ – \boldsymbol{\delta}_-$とおく。
以下、閉曲面$S$上の微小な面積$dS$について、この面積$dS$を通って、どれだけの分極電荷が閉曲面内へ流出したかを計算する。正電荷の流出量$dQ_+$、負電荷の流出量$dQ_-$は、電荷密度$\rho$と、面$dS$を通って流出した電荷のシートの体積の積であるから、法線ベクトルを$\boldsymbol{n}$として、
$$
dQ_+ = (+\rho) (\boldsymbol{\delta}_+ \cdot \boldsymbol{n}) dS
$$$$
dQ_- = (-\rho) (\boldsymbol{\delta}_- \cdot \boldsymbol{n}) dS
$$とかける。よって、この微小面$dS$から外へ出た合計の流出量$dQ_{out}$は、
$$
dQ_{out} = dQ_+ + dQ_- = \rho (\boldsymbol{\delta}_+ \cdot \boldsymbol{n}) dS – \rho (\boldsymbol{\delta}_- \cdot \boldsymbol{n}) dS = \rho (\boldsymbol{\delta}_+ – \boldsymbol{\delta}_-) \cdot \boldsymbol{n} dS = \rho (\boldsymbol{\delta} \cdot \boldsymbol{n}) dS
$$ここで、分極ベクトル$\boldsymbol{P}$の定義は、単位体積あたりの電気双極子モーメントであるので、電荷密度$\rho$のプラスとマイナスの流体が、距離$\boldsymbol{\delta}$だけズレたときの単位体積あたりのモーメント$\boldsymbol{P}(\boldsymbol{r})$は、$\boldsymbol{P} = \rho \boldsymbol{\delta}$とかける。これを先の式に代入すると、微小面$dS$から流出した電荷は、$dQ_{out} = \boldsymbol{P} \cdot \boldsymbol{n} dS$となるので、閉曲面$S$全体から流出した総電荷量$Q_{out}$は、
$$
Q_{out} = \oint_S \boldsymbol{P} \cdot \boldsymbol{n} dS
$$とかける。もともと、閉曲面$S$内部の電荷はゼロであったことを先に述べたので、そこから$Q_{out}$だけの電荷が流出したということは、閉曲面$S$内部に存在する電荷はその逆符号であるから、閉曲面$S$内に生じる分極電荷の合計を$q_p$とすると、
$$
q_p = -Q_{out} = – \oint_S \boldsymbol{P} \cdot \boldsymbol{n} dS
$$となる。右辺にガウスの発散定理を適用すると、
$$
q_p = \int_{V} \rho_p dV = -\int_{V} (\nabla \cdot \boldsymbol{P}) dV
$$となって、これが任意の体積$V$について成り立つには、被積分関数が恒等的に等しくなければならないため、以下が成立する。
$$
\rho_p(\boldsymbol{r}) = -\nabla \cdot \boldsymbol{P}(\boldsymbol{r})
$$□

定理２.４.Ｅ(物質中の電場におけるガウスの法則)
誘電体をプラスとマイナスのシートが重なり合ったモデルとみなしたとき、電場を$\boldsymbol{E}(\boldsymbol{r})$、電場によって生じた電気双極子モーメントの密度を分極ベクトル$\boldsymbol{P}(\boldsymbol{r})$、真電荷密度を$\rho_f(\boldsymbol{r})$とすると、
$$
\nabla \cdot \left( \epsilon_0 \boldsymbol{E}(\boldsymbol{r}) + \boldsymbol{P}(\boldsymbol{r}) \right) = \rho_f (\boldsymbol{r})
$$

定理２.４.Ｅの証明

誘電体中の真電荷密度を$\rho_f(\boldsymbol{r})$、分極によって生じる物質から取り出すことができない電荷を分極電荷密度を$\rho_p(\boldsymbol{r})$とするとき、全電荷密度は$\rho_{\text{total}} (\boldsymbol{r}) = \rho_f (\boldsymbol{r}) + \rho_p (\boldsymbol{r})$とかくことができる。先に述べたように、全電荷密度$\rho_{\text{total}} (\boldsymbol{r})$はもちろんマクスウェル方程式を満たすから、
$$
\nabla \cdot \boldsymbol{E}(\boldsymbol{r}) = \frac{\rho_{\text{total}}(\boldsymbol{r})}{\epsilon_0} = \frac{\rho_f (\boldsymbol{r}) + \rho_p (\boldsymbol{r})}{\epsilon_0}
$$となるので、両辺$\epsilon_0$をかけて整理すると、定理２.４.Ｄより以下が得られる。
$$
\nabla \cdot \left( \epsilon_0 \boldsymbol{E}(\boldsymbol{r}) + \boldsymbol{P}(\boldsymbol{r}) \right) = \rho_f (\boldsymbol{r})
$$□

ここで、$\epsilon_0 \boldsymbol{E}(\boldsymbol{r}) + \boldsymbol{P}(\boldsymbol{r})$はその発散が真電荷密度に比例するという意味で重要であるため、これを物理量として定義します。重ねて言いますが、定理２.４.Ｅの形の表式が$\nabla \cdot \boldsymbol{E}(\boldsymbol{r}) = \frac{\rho_{\text{total}}(\boldsymbol{r})}{\epsilon_0}$の形の表式よりも、物質中の電場を求めるときに使いやすいのは、全電荷よりも設定した真電荷の方がわかりやすいからです。

定義２.４.Ｆ(電束密度の定義)
電場$\boldsymbol{E}$と、分極ベクトル(電場によって生じた電気双極子モーメントの密度)$\boldsymbol{P}$に対して、電束密度$\boldsymbol{D}$を次のように定義する。
$$
\boldsymbol{D} = \epsilon_0 \boldsymbol{E} + \boldsymbol{P}
$$

さて、ここで、電束密度$\boldsymbol{D}$と電場$\boldsymbol{E}$の向きが一致するか、つまり、分極ベクトル$\boldsymbol{P}$と電場$\boldsymbol{E}$の向きが一致するかは条件によってまちまちで、結晶のように方向性のある物質であったり、非常に強い電場がかかっていたりなどしているときは一致しないことも多いです。ただ一致する場合も多く、この場合には非常に扱いやすくなりますから、一致する場合について、物質依存の物理量を次のように定義します。

定義２.４.Ｇ(電気感受率、誘電率、比誘電率の定義)
分極ベクトル$\boldsymbol{P}$と電場$\boldsymbol{E}$の向きが一致しているとき、$\boldsymbol{P}= \chi_e \boldsymbol{E}$なる$\chi_e$を電気感受率、$\boldsymbol{D}= \epsilon \boldsymbol{E}$なる$\epsilon= \epsilon_0 + \chi_e$を誘電率、物質の誘電率$\epsilon$の真空の誘電率$\epsilon_0$に対する比$\epsilon_r= \epsilon / \epsilon_0$を比誘電率と定義する。

定義２.４.Ｇについては必ずすべての誘電体に定義できるわけではないので、誘電体における静電場を見るときに原則となるのは、定理２.４.Ｃ,Ｄ,Ｅで与えている式になります。
本稿で扱った定理２.４.Ｃ,Ｄ,Ｅと静電場における渦なしの法則を用いて考える、誘電体の境界条件については別稿で扱っています。
＞＞誘電体における境界条件

磁性体における静磁場

誘電体内部に電気双極子モーメントが生じる分極とよく似ている現象として、磁性体内部に磁気双極子モーメントが生じる磁化があります。
物質が磁気を帯びる根本的な原因は、原子の中にある電子の動きにあります。電子は軌道運動あるいはスピンという性質によって、回転電流を生じさせており、これが磁気双極子モーメントをつくっています。通常、物質内ではこれらの微小な磁石がバラバラの方向を向いていたり、ペアになって互いに打ち消し合ったりしているため、全体としては磁力を持ちませんが、外部から磁場をかけると、その影響を受けて状態が変化するのです。現実の磁化の現象は大きく次の三つに分けられます。

(1)常磁性：通常、電子は2つペアになってスピンを打ち消し合うといいましたが、物質によってはペアにならずに余っている電子(不対電子)を持つものがあります。この不対電子はそれぞれが独立した磁石として振る舞い、外部から磁場がかかると磁場の方向に整列しようとします。
アルミニウム、酸素などの物質がこれにあてはまり、外部磁場と同じ向きに磁化します。

(2)強磁性：常磁性のなかでも特殊なもので、不対電子どうしが量子力学的な力でつねに整列するため、外部磁場がなくなっても磁力が残る(永久磁石になる)性質です。
鉄やニッケルなどの物質がこれにあてはまり、外部磁場と同じ向きに強く磁化します。

(3)反磁性：不対電子が存在しない原子については、コイルに磁石を近づけたときに逆向きの電流が流れて反発する電磁誘導のように、外部から磁場がかかると電子がその磁場の変化を打ち消そうとする方向に軌道運動を変化させます(実はすべての原子でこの軌道運動の変化は起こるのですが効果が弱く、常磁性や強磁性が強い場合は隠れてしまいます)。
水、銅、金、銀、ガラスなどの物質がこれにあてはまり、外部磁場と逆向きに磁化します。

磁性体の磁化によって生じる電流を磁化電流といい、磁化電流に対して、これまで扱ってきたふつうの電荷の運動によって生じる電流を真電流といいます。

磁性体をよく説明するのは、物質中に微小な「原子サイズの電流ループ」がびっしり敷き詰められているとみなすモデルです。「原子サイズの電流ループ」というのは電子の回転運動のモデルで、これは磁性体中で一様である必要はなく、隣り合うループが接する面で電流を打ち消したり強めたりして、表面および内部に磁化表面電流および磁化体積電流を生じさせます。
なお、ミクロにみると電流ループが磁化ベクトルをつくっていますが、以下、表現の関係で磁化ベクトルが電流ループをつくるというような言い回しをすることがあります。

定理２.４.４.７より回転電流は、そのサイズに比べて十分遠方では、電流と閉回路の面積の積を大きさとする、電流の向きに右ねじを回して進む方向の磁気双極子モーメント$\boldsymbol{m}$をもつ磁気双極子と等価として扱うことができます。さて、磁性体をこのようなモデルであるとみなすとき、以下の定理が成り立ち、それらは現実をよく説明しています。

定理２.４.Ｈ(磁化表面電流密度)
磁性体を微小な電流ループが敷き詰められているモデルとみなしたとき、磁性体表面のある位置$\boldsymbol{r}$における磁化表面電流密度を$\boldsymbol{K}_m(\boldsymbol{r})$とすると、
$$
\boldsymbol{K}_m(\boldsymbol{r}) = \boldsymbol{M}(\boldsymbol{r}) \times \boldsymbol{n}(\boldsymbol{r})
$$となる。ただし、磁化ベクトル$\boldsymbol{M}(\boldsymbol{r})$は、位置$\boldsymbol{r}$における電流によって生じた磁気双極子モーメントの密度、法線ベクトル$\boldsymbol{n}(\boldsymbol{r})$は、磁性体表面に垂直な単位ベクトルである。

定理２.４.Ｈの証明

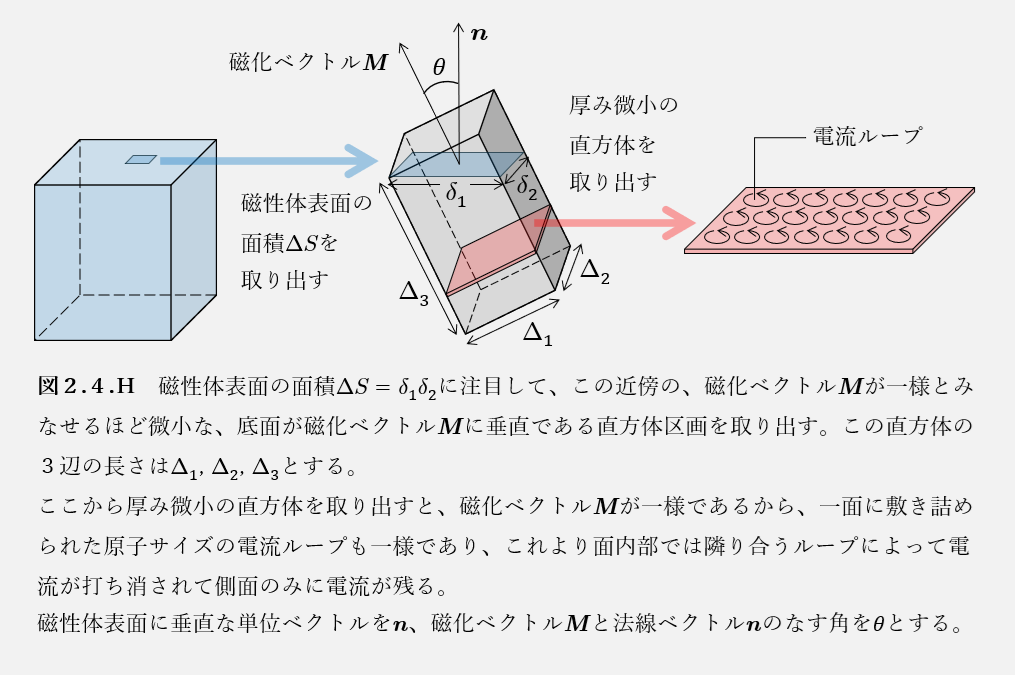
図２.４.Ｈのように、磁性体表面の面積$dS=\delta_1 \delta_2$に注目して、この近傍の、磁化ベクトル$\boldsymbol{M}$が一様とみなせるほど微小な、底面が磁化ベクトル$\boldsymbol{M}$に垂直である直方体区画を取り出す。この直方体の３辺の長さを$\Delta_1$, $\Delta_2$, $\Delta_3$とする。
この直方体区画の磁気双極子モーメント$m$は、磁気双極子モーメントの密度を磁化ベクトル$\boldsymbol{M}$と定義していることから、$m=M\Delta_1 \Delta_2 \Delta_3$とかける一方で、この直方体区画は側面のみに面電流が残るため、この区画の側面をめぐる合計の定常電流を$I$とすると、定理２.４.４.７より$m=I\Delta_1 \Delta_2$とかける。したがって、$m=M\Delta_1 \Delta_2 \Delta_3 = I\Delta_1 \Delta_2$より、$M\Delta_3=I$、つまり$M$は側面を流れる単位高さあたりの電流となる。$\Delta_3 = \delta_1 \sin \theta$であるので、
$$
\boldsymbol{K}_m = \frac{I}{\delta_1} = \frac{M \Delta_3}{\delta_1} = \frac{M (\delta_1 \sin \theta)}{\delta_1} = M \sin \theta
$$とかける。向きについては、表面近くに並ぶ小さな電流ループについて、隣同士が打ち消されずにループの外周の一部だけ残る方向は表面に接する成分である$\boldsymbol{M} \times \boldsymbol{n}$の方向であるから、外積の定義より以下が得られる。
$$
\boldsymbol{K}_m = \boldsymbol{M} \times \boldsymbol{n}
$$□

定理２.４.Ｉ(磁化体積電流密度)
磁性体を微小な電流ループが敷き詰められているモデルとみなしたとき、磁性体内部のある位置$\boldsymbol{r}$における磁化体積電流密度を$\boldsymbol{J}_m(\boldsymbol{r})$とすると、
$$
\boldsymbol{J}_m(\boldsymbol{r}) = \nabla \times \boldsymbol{M}(\boldsymbol{r})
$$となる。ただし、磁化ベクトル$\boldsymbol{M}(\boldsymbol{r})$は、位置$\boldsymbol{r}$における電流によって生じた磁気双極子モーメントの密度である。

定理２.４.Ｉの証明

磁化ベクトル$\boldsymbol{M}$は、
$$
\boldsymbol{M}(x,y,z) = M_x(x,y,z){\boldsymbol{e}_x} + M_y(x,y,z){\boldsymbol{e}_y} + M_z(x,y,z){\boldsymbol{e}_z}
$$と成分に分解することができるから、磁化ベクトルがつくる磁化電流は、$M_x(x,y,z)$がつくる磁化電流、$M_y(x,y,z)$がつくる磁化電流、$M_z(x,y,z)$がつくる磁化電流の和となっていることがわかる。ここでまず、$M_z(x,y,z)$がつくる磁化電流を考えましょう。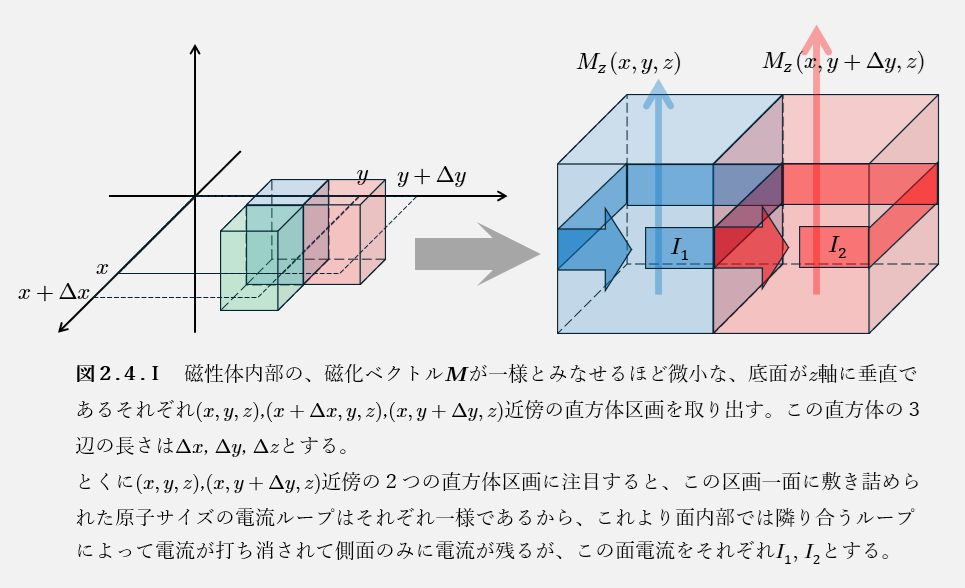

図２.４.Ｉのように、磁性体内部の、磁化ベクトル$\boldsymbol{M}$が一様とみなせるほど微小な、底面が$z$軸に垂直であるそれぞれ$(x,y,z)$,$(x+\Delta x,y,z)$,$(x,y+\Delta y,z)$近傍の直方体区画を取り出して、磁化ベクトル$M_z(x,y,z)$, $M_z(x+\Delta x,y,z)$, $M_z(x,y+\Delta y,z)$がつくる電流を考える。
まず、$(x,y,z)$,$(x,y+\Delta y,z)$近傍の２つの直方体区画に注目すると、この2つの箱の境界面(接している面)を流れている表面電流密度は、$I_2-I_1$である。定理２.４.Ｈより、表面電流密度について、
$$
-I_1 = (M_z(y)\boldsymbol{e}_z) \times \boldsymbol{e}_y = -M_z(y)\boldsymbol{e}_x
$$$$
I_2 = (M_z(y+\Delta y)\boldsymbol{e}_z) \times (-\boldsymbol{e}_y) = M_z(y+\Delta y)\boldsymbol{e}_x
$$であるから、境界面の高さ$\Delta z$の区間を流れる電流は、これを足し合わせて以下のようになる。
$$
\Delta I_x = \left[ M_z(y+\Delta y) – M_z(y) \right] \Delta z = \approx \frac{\partial M_z}{\partial y} \Delta y \Delta z
$$同様に、$(x,y,z)$, $(x+\Delta x,y,z)$近傍の２つの直方体区画に注目すると、この2つの箱の境界面(接している面)に以下を残す。
$$
\Delta I_y = -\left[ M_z(x+\Delta y) – M_z(x) \right] \Delta z = \approx -\frac{\partial M_z}{\partial x} \Delta x \Delta z
$$つまり、$\boldsymbol{M}_z$の変化が生み出す電流$\boldsymbol{I}(\boldsymbol{M}_z)$は、
$$
\boldsymbol{I}(\boldsymbol{M}_z) = \left( \frac{\partial M_z}{\partial y} \Delta y \Delta z \right) \boldsymbol{e}_x – \left( \frac{\partial M_z}{\partial x} \Delta x \Delta z \right) \boldsymbol{e}_y
$$という形でかける。同様に、$\boldsymbol{M}_y$の変化が生み出す電流$\boldsymbol{I}(\boldsymbol{M}_y)$は、
$$
\boldsymbol{I}(\boldsymbol{M}_y) = -\left( \frac{\partial M_y}{\partial z} \Delta z \Delta y \right) \boldsymbol{e}_x + \left( \frac{\partial M_y}{\partial x} \Delta x \Delta y \right) \boldsymbol{e}_z
$$とかけ、$\boldsymbol{M}_x$の変化が生み出す電流$\boldsymbol{I}(\boldsymbol{M}_x)$は、
$$
\boldsymbol{I}(\boldsymbol{M}_x) = \left( \frac{\partial M_x}{\partial z} \Delta z \Delta x \right) \boldsymbol{e}_y – \left( \frac{\partial M_x}{\partial y} \Delta y \Delta x \right) \boldsymbol{e}_z
$$とかける。全電流$\boldsymbol{I}_{total}$は、これら3つの和であって、各要素を通過する面積で割って、電流密度$\boldsymbol{J}_m$とすると、
$$
(J_m)_x = \frac{\partial M_z}{\partial y} – \frac{\partial M_y}{\partial z} = \left[ \nabla \times \boldsymbol{M} \right]_x
$$$$
(J_m)_y = \frac{\partial M_x}{\partial z} – \frac{\partial M_z}{\partial x} = \left[ \nabla \times \boldsymbol{M} \right]_y
$$$$
(J_m)_z = \frac{\partial M_y}{\partial x} – \frac{\partial M_x}{\partial y} = \left[ \nabla \times \boldsymbol{M} \right]_z
$$とかけるので、以下が成立する。
$$
\boldsymbol{J}_m = \nabla \times \boldsymbol{M}
$$□

定理２.４.Ｊ(物質中の磁場におけるアンペールの法則)
磁性体を微小な電流ループが敷き詰められているモデルとみなしたとき、磁場を$\boldsymbol{B}(\boldsymbol{r})$、磁場によって生じた磁気双極子モーメントの密度を磁化ベクトル$\boldsymbol{M}(\boldsymbol{r})$、真電流密度を$\boldsymbol{j}_f(\boldsymbol{r})$とすると、
$$
\nabla \times \left( \frac{1}{\mu_0}\boldsymbol{B}(\boldsymbol{r}) – \boldsymbol{M}(\boldsymbol{r}) \right) = \boldsymbol{J}_f(\boldsymbol{r})
$$

定理２.４.Ｊの証明

磁性体中の真電流密度を$\boldsymbol{j}_f(\boldsymbol{r})$、磁化によって生じる電子の運動による電流である磁化電流密度を$\boldsymbol{j}_m(\boldsymbol{r})$とするとき、全電流密度は$\boldsymbol{j}_{\text{total}} (\boldsymbol{r}) = \boldsymbol{j}_f (\boldsymbol{r}) + \boldsymbol{j}_m (\boldsymbol{r})$とかくことができる。先に述べたように、全電流密度$\boldsymbol{j}_{\text{total}} (\boldsymbol{r})$はもちろんマクスウェル方程式を満たすから、
$$
\nabla \times \boldsymbol{B}(\boldsymbol{r}) = \mu_0 \boldsymbol{j}_{\text{total}} (\boldsymbol{r}) = \mu_0 \{ \boldsymbol{j}_f (\boldsymbol{r}) + \boldsymbol{j}_m (\boldsymbol{r}) \}
$$となるので、両辺$\mu_0$をかけて整理すると、定理２.４.Ｉより以下が得られる。
$$
\nabla \times \left( \frac{1}{\mu_0}\boldsymbol{B}(\boldsymbol{r}) – \boldsymbol{M}(\boldsymbol{r}) \right) = \boldsymbol{J}_f(\boldsymbol{r})
$$□

ここで、$ \frac{1}{\mu_0}\boldsymbol{B}(\boldsymbol{r}) – \boldsymbol{M}(\boldsymbol{r}) $はその回転が真電流密度に比例するという意味で重要であるため、これを物理量として定義します。重ねて言いますが、定理２.４.Ｉの形の表式が$\nabla \times \boldsymbol{B}(\boldsymbol{r}) = \mu_0 \boldsymbol{j}_{\text{total}} (\boldsymbol{r})$の形の表式よりも、物質中の磁場を求めるときに使いやすいのは、全電流よりも設定した真電流の方がわかりやすいからです。

定義２.４.Ｋ(磁場の強さの定義)
磁場$\boldsymbol{B}$と、磁化ベクトル(磁場によって生じた磁気双極子モーメントの密度)$\boldsymbol{M}$に対して、磁場の強さ$\boldsymbol{H}$を次のように定義する。
$$
\boldsymbol{H} = \frac{1}{\mu_0}\boldsymbol{B} – \boldsymbol{M}
$$

さて、ここで、磁場の強さ$\boldsymbol{H}$と磁場$\boldsymbol{B}$の向きが一致するか、つまり、磁化ベクトル$\boldsymbol{M}$と磁場$\boldsymbol{B}$の向きが一致するかは条件によってまちまちで、鉄などの強磁性体であったり、非常に強い磁場がかかっていたりなどしているときは一致しないことも多いです。ただ一致する場合も多く、この場合には非常に扱いやすくなりますから、一致する場合について、物質依存の物理量を次のように定義します。

定義２.４.Ｌ(磁化率、透磁率、比透磁率の定義)
磁化ベクトル$\boldsymbol{M}$と磁場$\boldsymbol{B}$の向きが一致しているとき、$\boldsymbol{P}= \chi_m \boldsymbol{H}$なる$\chi_m$を磁化率、$\boldsymbol{B}= \mu \boldsymbol{H}$なる$\mu= \mu_0 + \chi_m$を透磁率、物質の透磁率$\epsilon$の真空の透磁率$\mu_0$に対する比$\mu_r= \mu / \mu_0$を比透磁率と定義する。

定義２.４.Ｌについては電場のときと同様に、必ずすべての磁性体に定義できるわけではないので、磁性体における静磁場を見るときに原則となるのは、定理２.４.Ｈ,Ｉ,Ｊで与えている式になります。
本稿で扱った定理２.４.Ｈ,Ｉ,Ｊと静磁場におけるガウスの法則を用いて考える、誘電体の境界条件については別稿で扱っています。
＞＞磁性体における境界条件

物質中の変動する電磁場

誘電体や磁性体における電磁場

まず確認ですが、物質中の電磁場については特別で、マクスウェル方程式が成り立たないとかいうわけではありません。マクスウェル方程式は物質中においても、厳密に正しいです。ただ物質中の原子や分子をすべて計算するのは現実的に不可能であるため、マクスウェル方程式に必要な、全電荷分布$\rho$や全電流分布$\boldsymbol{j}$を求めることができないのが問題というわけです。
そこで、人間がおいた真電荷分布$\rho_f$や真電流分布$\boldsymbol{j}_f$をもとに電磁場を求める方程式があれば便利だということで、以下の物質中のマクスウェル方程式が組まれています。

定理２.４.Ｍ(物質中のマクスウェル方程式)
誘電体をプラスとマイナスのシートが重なり合ったモデルとみなし、磁性体を微小な電流ループが敷き詰められているモデルとみなしたとき、物質中の電場$\boldsymbol{E}$、磁場$\boldsymbol{B}$に対し、電束密度$\boldsymbol{D}$を$\boldsymbol{D} = \epsilon_0 \boldsymbol{E} + \boldsymbol{P}$、磁場の強さ$\boldsymbol{H}$を$\boldsymbol{H} = \frac{1}{\mu_0}\boldsymbol{B} – \boldsymbol{M}$と定義すると、以下が成立する。
$$
\nabla \cdot \boldsymbol{D} = \rho_f
$$$$
\nabla \cdot \boldsymbol{B} = 0
$$$$
\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}
$$$$
\nabla \times \boldsymbol{H} = \boldsymbol{j}_f + \frac{\partial \boldsymbol{D}}{\partial t}
$$ただし、$\epsilon_0$は真空の誘電率、$\mu_0$は真空の透磁率、$\rho_f$は真電荷密度、$\boldsymbol{j}_f$は真電流密度、分極ベクトル$\boldsymbol{P}$は電気双極子モーメントの密度、磁化ベクトル$\boldsymbol{M}$は磁気双極子モーメントの密度である。

定理２.４.Ｍの証明

第２式$\nabla \cdot \boldsymbol{B} = 0$と第３式$\nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B}}{\partial t}$については、原理２.４のマクスウェル方程式そのままであるので、第１式と第４式のみ証明する。
さて、まず空間に存在する全電荷密度$\rho_{total}$と全電流密度$\boldsymbol{J}_{total}$の成分を書き出す。全電荷密度$\rho_{total}$は、電荷が運動しているときも変わらず、真電荷$\rho$と分極電荷$\rho_p$の和になる一方で、全電流密度$\boldsymbol{J}_{total}$は、真電流$\boldsymbol{j}$と磁化電流$\boldsymbol{J}_m$、それに加えて、分極電荷$\rho_p$の時間変化によって生じる電流である分極電流$\boldsymbol{J}_p$の和になる。
分極電荷$\rho_p$と磁化電流$\boldsymbol{J}_m$に関しては、定理２.４.Ｄや定理２.４.Ｉの導出方法は電磁場が変動していようと使えるため、分極体積電荷密度を$\rho_p$、磁化体積電流密度を$\boldsymbol{J}_m$とすると、以下が成り立つ
$$
\rho_p(\boldsymbol{r}) = – \nabla \cdot \boldsymbol{P}(\boldsymbol{r})
$$$$
\boldsymbol{J}_m(\boldsymbol{r}) = \nabla \times \boldsymbol{M}(\boldsymbol{r})
$$また、プラスとマイナスのシートが重なり合った誘電体のモデルにおいて、シートの変位を$\boldsymbol{u}$とすると、分極電流は$\boldsymbol{J}_p = \rho \frac{d\boldsymbol{u}}{dt}$とかける。分極ベクトル$\boldsymbol{P}$の定義は、単位体積あたりの電気双極子モーメントであるので、電荷密度$\rho$のプラスとマイナスの流体が、距離$\boldsymbol{u}$だけズレたときの単位体積あたりのモーメント$\boldsymbol{P}$は、$\boldsymbol{P} = \rho \boldsymbol{u}$とかけるので、これより、$\frac{\partial \boldsymbol{P}}{dt}$である。

したがって、全電荷密度$\rho_{total}$、全電流密度$\boldsymbol{J}_{total}$は、
$$
\rho_{total} = \rho_f + \rho_p = \rho_f – \nabla \cdot \boldsymbol{P}
$$$$
\boldsymbol{J}_{total} = \boldsymbol{j}_f + \boldsymbol{J}_m + \boldsymbol{J}_p = \boldsymbol{j}_f + \nabla \times \boldsymbol{M} + \frac{\partial \boldsymbol{P}}{\partial t}
$$とかくことができる。第１式については、真空中のガウスの法則$\nabla \cdot \boldsymbol{E} = \frac{\rho_{total}}{\epsilon_0}$に$\rho_{total} = \rho – \nabla \cdot \boldsymbol{P}$を代入して整理すると、$\nabla \cdot \boldsymbol{D} = \rho$が示される。第４式についても、真空中のアンペール-マクスウェルの法則$\nabla \times \boldsymbol{B} = \mu_0 \left( \boldsymbol{J}_{total} + \epsilon_0 \frac{\partial \boldsymbol{E}}{\partial t} \right)$を代入して整理すると、$\nabla \times \boldsymbol{H} = \boldsymbol{j}_f + \frac{\partial \boldsymbol{D}}{\partial t}$が示される。□

さらに具体的な物質のモデルを仮定すると、マクスウェル方程式を用いて、物質中の電磁波などについて考えることができます。これについては別稿で扱っています。
＞＞誘電体や磁性体における電磁場

導体における電磁場

さて、変動する電磁場をかけられた導体を考えてみましょう。静電場のときは導体内部のあらゆる位置$\boldsymbol{r}$において、静電場$\boldsymbol{E}(\boldsymbol{r})=\boldsymbol{0}$となるということで納得しましたが、変動する電磁場においてはその限りではありません。導体といえども、原子核と内殻電子の格子(プラスのイオン格子)があって、これらが電場でわずかに歪む(分極する)効果は、$\boldsymbol{P}$として $\boldsymbol{D}$の中にひっそりと含まれています。
このため、導体の自由電子のつくる電荷分布や電流分布をそれぞれ真電荷分布や真電流分布として、導体の自由電子を除いた部分を誘電体や磁性体と考えたとき、先と同様に定理２.４.Ｍ(物質中のマクスウェル方程式)が適用できるといえます。再掲します。

大事なことなので言い換えると、導体という特別な物質があるわけではなく、むしろ「誘電体であって磁性体である物質の中に、たまたま束縛されずに自由に動くことができる電荷が混ざっている状態として記述して、その自由に動くことができる電荷がつくる電荷分布や電流分布を真電荷分布や真電流分布と扱う」ということです。

さらに具体的なモデルを仮定すると、マクスウェル方程式を用いて、導体中の電磁波などについて考えることができます。これについては別稿で扱っています。
人間がおいた真電荷分布$\rho_f$や真電流分布$\boldsymbol{j}_f$をもとに電磁場を求める方程式があれば便利だということで、物質中のマクスウェル方程式を組んだのにも関わらず、導体の自由電子のつくる電荷分布や電流分布をそれぞれ真電荷分布や真電流分布とすると、これも簡単には求められないから物質中のマクスウェル方程式を導体に適用する意味がないのではないか、、、とかいう疑問もこの稿で解決するかもしれません。
＞＞導体における電磁場