クーロンの法則を仮定したときの、電場における渦なしの法則の証明

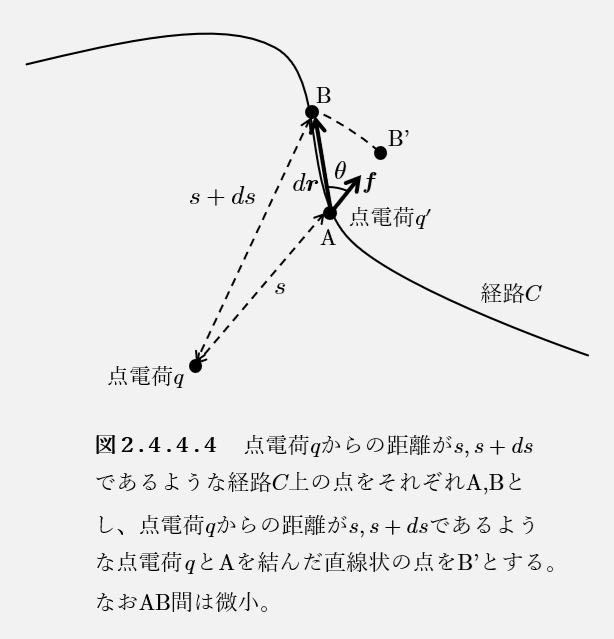
図２.４.４.４のように、点\(A\)、点\(B\)、点\(B’\)を定めるとき、ある経路\(C\)の微小区間、点\(A\)から点\(B\)上で電荷\(q’\)を動かすときの、静電気力のする仕事\(dw\)は、
$$
dw=\mathbf{f}(s) \cdot d\boldsymbol{r}=f(s)dr\cos\theta
$$一方で、微小区間、点\(A\)から点\(B’\)上で電荷\(q’\)を動かすときの、静電気力のする仕事\(dw’\)は、力の向きと移動方向が同じであるため、
$$
dw’={f}(s) ds=f(s)dr\cos\theta \quad (∵ ds=dr \cos\theta)
$$ゆえに任意の経路\(C\)上の、点電荷\(q\)からの距離が\(s\)である点と\(s+ds\)である点を結ぶ微小区間での仕事は、点電荷\(q\)からの距離が\(s\)である任意の点を始点に、点電荷\(q\)からの距離が\(s+ds\)になるまで直線的に離れるような微小経路における仕事と等しい。したがって、十分な長さの経路における仕事は、微小経路における仕事の寄せ集めとみなせるので、任意の経路\(C\)上の、点電荷\(q\)からの距離が\(a\)である点と\(b\)である点を結ぶ経路での仕事は、点電荷\(q\)からの距離が\(a\)である任意の点を始点に、点電荷\(q\)からの距離が\(b\)になるまで直線的に離れるような直線経路における仕事と等しくなる。すなわち、仕事の値は、始点と終点の点電荷からの距離が同じであれば等しいことが示された。□

任意の電荷分布は、微小空間に分けていくと点電荷の集まりとみなせるので、ある電荷分布について点電荷\(q_1\),\(q_2\),…\(q_i\),…の集まりとして扱える。このとき、\(q_1\),\(q_2\),…\(q_i\),…がそれぞれ単独で作る電場を\(\boldsymbol{e}_1\),\(\boldsymbol{e}_2\),…\(\boldsymbol{e}_i\),…とすると、始点\(X\)から終点\(Y\)まで任意の２経路\(C\),\(C’\)で電荷\(q’\)を動かしたときの、静電気力のする仕事は、
$$
\displaystyle \int_{C} q’\boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r} = \displaystyle \int_{C} q’ \left( \sum_i\boldsymbol{e}_i(\boldsymbol{r}) \right) \cdot d\boldsymbol{r} = \sum_i \displaystyle \int_{C} q’\boldsymbol{e}_i(\boldsymbol{r}) \cdot d\boldsymbol{r} = \sum_i \displaystyle \int_{C’} q’\boldsymbol{e}_i(\boldsymbol{r}) \cdot d\boldsymbol{r} = \displaystyle \int_{C’} q’ \left( \sum_i\boldsymbol{e}_i(\boldsymbol{r}) \right) \cdot d\boldsymbol{r} = \displaystyle \int_{C’} q’\boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r}
$$より等しくなる。すなわち、クーロン力は保存力であることが示された。□

補題２.４.４.５より、クーロン力は保存力であることから、単位電荷に対する始点と終点が等しい経路における仕事\(\oint_C \boldsymbol{E}(\boldsymbol{r}) \cdot d\boldsymbol{r}\)は、単位電荷を動かさないときの仕事とつねに等しいので、０である。□