こんにちは、turtleです。現在電磁気学を学んでおりまして、その備忘録のような形でこのブログを書かせていただいております。基本的に大学の内容となっていますが、数式さえ乗り越えれば高校生でも理解できると思っていますので、どうぞよろしくお願いいたします。
導体中の自由電子が電場から力を受けてその力の方向に動くような理想的なモデルでは、電流はその点の電場に比例したベクトルになります。この法則をオームの法則といいます。
積分形のオームの法則
オームの法則は、中学理科のころから扱っている法則で、おなじみのものだと思います。
積分形のオームの法則
導線に対してその両端に電位差\(\Delta \phi\)をかけたとき、流れる電流\(I\)は、導線の具体的な構造や温度によって定まる定数である電気抵抗\(R\)を用いて、以下のようにかける。
$$
I=\frac{\Delta \phi}{R}
$$
ここでかいた表式を積分形のオームの法則とよびます。これはクーロンの法則などから導かれる法則ではなく、遠隔作用の立場で見たマクロな関係を記述した実験則であるので、本稿ではこれが成り立つことを認めたうえで、微分形のオームの法則の記述について考えていきます。
微分形のオームの法則
以下のように記述する。ただし、\(\boldsymbol{i}(\boldsymbol{r})\)は各位置\(\boldsymbol{r}\)での電流密度を、\(\sigma\)は導体の電気伝導度を表す。
$$
\boldsymbol{i}(\boldsymbol{r})=\sigma \boldsymbol{E}(\boldsymbol{r})
$$
証明 積分形のオームの法則から、微分形のオームの法則を示す。
まず導線の電気抵抗\(R\)に関して考える。導線の長さを\(k\)倍にしてその両端に電位差\(\Delta \phi\)をかけたとき、もとの導線の長さの区間には電位差\(\frac{\phi}{k}\)がかかるので、この導線を流れる電流はもとの\(\frac{1}{k}\)倍になる、すなわち積分形のオームの法則より電気抵抗は\(k\)倍になっている。
一方で、導線の断面積を\(k\)倍にしてその両端に電位差\(\Delta \phi\)をかけたとき、この導線を流れる電流はもとの\(k\)倍になる、すなわち積分形のオームの法則より電気抵抗は\(\frac{1}{k}\)倍になっている。
これより、導線の電気抵抗\(R\)は、導線の長さ\(l\)に比例し、導線の断面積\(S\)に反比例することがわかるので、導線の具体的な構造や温度によって定まる定数である抵抗率\(\rho\)を用いて、
$$
R=\rho \frac{l}{S}
$$とかくことができるとわかる。
導線を流れる一様な電流\(I\)は電流密度\(i\)に対して、その定義より\(I=iS\)とかけ、導線両端の電位差\(\Delta \phi\)も一様電場\(E\)に対して、その定義より\(\Delta \phi=El\)とかける。
ゆえに積分形のオームの法則にこれらを代入すると、
$$
iS=\frac{El}{\rho \frac{l}{S}}
$$整理すると\(i=\frac{1}{\rho} E\)となり、電流と電場の向きが一般に同じことをふまえると、\(\rho\)の逆数を\(\sigma\)としたとき、
$$
\boldsymbol{i}(\boldsymbol{r})=\sigma \boldsymbol{E}(\boldsymbol{r})
$$とかけ、これより示された。□
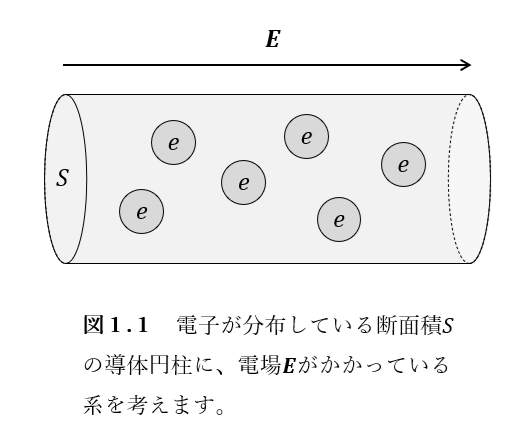
別の証明 導体中を流れる電流を定量化して考える単純なモデルとして、図１のように断面積\(S\)の導体円柱内部に、数密度\(n\)で電子が分布している系を考える。導体内部を電子が運動すると、導体中の分子に衝突するなどして抵抗を受けるが、これを速度に比例する比例係数\(\alpha\)の抵抗力で近似することにする。
ここで、この導体に電場\(\boldsymbol{E}\)をかけたとすると、導体内部の電子はそれぞれ電気的に\(-e \boldsymbol{E}\)の力を受けるので、抵抗力とあわせて、運動方程式を立てると、
$$
m \frac{d \boldsymbol{v}}{dt}=-e \boldsymbol{E} -\alpha \boldsymbol{v}
$$これは\(\boldsymbol{v}\)に関する１階微分方程式であるので、厳密に解くことができる。はじめ(\(t=0\))で静止していたとすると、
$$
\boldsymbol{v}=\frac{-e}{\alpha}\boldsymbol{E}(1+e^{-\frac{\alpha}{m}t})
$$と表せ、十分時間がたったとき電子の速度は\(\frac{-e}{\alpha}\boldsymbol{E}\)に収束する。
一方で、電流\(\boldsymbol{I}\)は、正電荷の流れる方向を向き、単位時間あたりに通過する電荷量を大きさとするベクトル量として定義されるので、電子が単位時間で\(v\)だけ進むことをふまえると、ある断面を単位時間あたりに通過する電子の数は、その断面から電子の進行方向とは逆の向きに距離\(v\)だけ進んだところまでの体積\(Sv\)の円柱に含まれる電子の数\(nSv\)に等しくなる。
電流の向きと電子の進む向きは逆であるので、
$$
\boldsymbol{I}=-enS \boldsymbol{v}
$$として表され、電流密度は定義よりこれを\(S\)で割ったものになる。
これらの速度と電流の表式から、導体中における電流密度\(\boldsymbol{i}\)は、
$$
\boldsymbol{i}=\frac{ne^2}{\alpha}\boldsymbol{E}
$$と表せる。\(\frac{ne^2}{\alpha}\)は導体の具体的な構造や温度などによって定まる定数で、これを電気伝導度\(\sigma\)とすると、
$$
\boldsymbol{i}(\boldsymbol{r})=\sigma \boldsymbol{E}(\boldsymbol{r})
$$とかけ、これより示された。□
なお、これらは初めに述べたように単純なモデルであって、電流に大きく影響を及ぼさないさまざまな要素を考慮していません。たとえば、自由電子は導体に電場をかけていないときもつねに動き回っており、はじめのモデルで扱っている速さというのは電子の平均的な速さになります。また、電流が厳密に電場と同じ方向に流れるかどうかは物質に依り、実は方向性のある結晶構造などでは近似的にしか成り立たないのです。
以上、オームの法則の積分形および微分形の記述と、その証明になります。
コメント